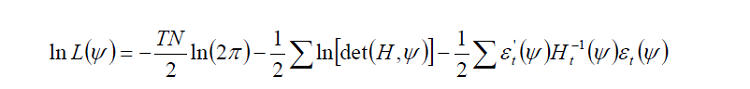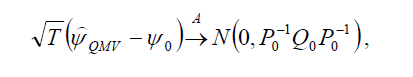En faisant référence à Gouriéroux (1997) à Bollerslev et Wooldridge (1996) on peut dire que sous l’hypothèse de la normalité de la distribution conditionnelle multivariée, la fonction de vraisemblance est formalisée comme suit :
Où ψ est le vecteur de paramètres inconnus et T et le nombre d’observations. Or, comme on l’a vu dans la section réservée aux propriétés des séries financières l’hypothèse de la normalité est souvent rejetée. L’estimation est effectuée suivant la méthode du maximum de vraisemblance.
L’estimateur du maximum de vraisemblance est :
Où ψ0 est le vrai vecteur de paramètres.
Le test de maximum de vraisemblance est subdivisé en trois tests :
– Le test de Wald ;
– Le test de Multiplicateur de Lagrange (LN) ;
– Le test de Ratio de vraisemblance (LR).
Les trois tests sont asymptotiquement distribués selon une loi de χ²r
Où r est le nombre de conditions sous l’hypothèse nulle H0. En échantillon fini il est démontré qu’en valeur numérique on a :
LN ≤ LR ≤Wald ce qui implique que Wald est plus puissant car on rejette plus l’hypothèse H0. Cependant, on n’utilise pas simplement le test de Wald car au départ on ne connaît pas la vraie distribution.
Page suivante : 2.11 Méthodologie du test de MEDAF
Retour au menu : INTEGRATION FINANCIÈRE ET DIVERSIFICATION INTERNATIONALE