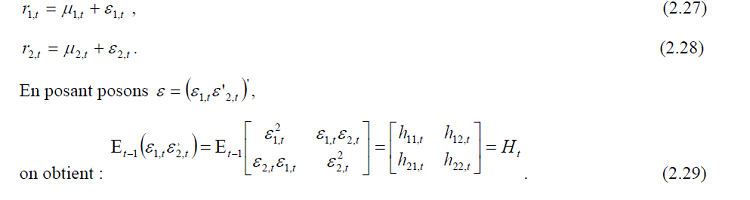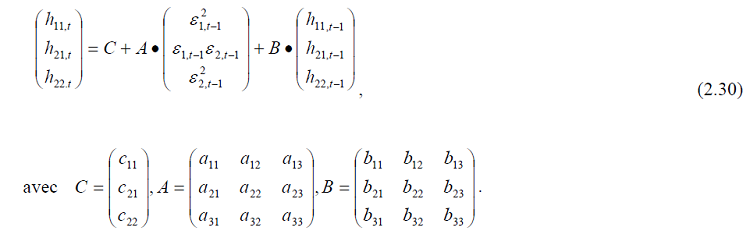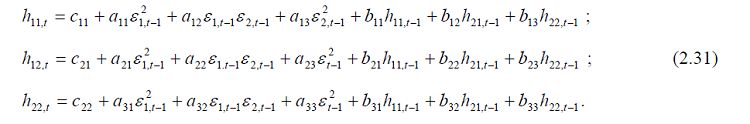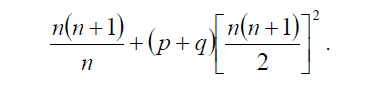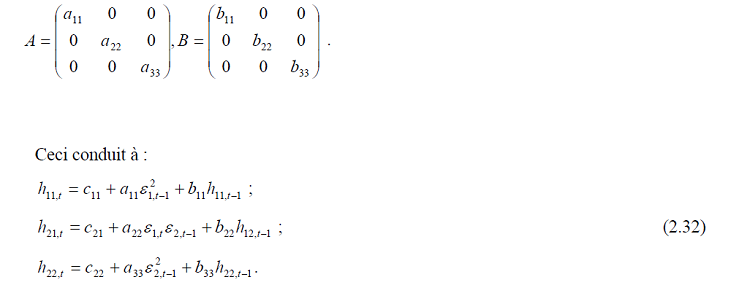Le modèle GARCH multivarié constitue la clé de voûte de notre travail, raison pour laquelle nous jugeons indispensable de faire une circonscription sommaire des différentes modélisations GARCH multivariées dans le but d’exposer tous les cas de figure. Cependant, nous avons délibérément exclu le modèle à corrélations conditionnelles constantes (CCC-GARCH) et le modèle de corrélation conditionnelle dynamique (DCC-GARCH) car ils ne s’inscrivent pas dans le cadre de cette étude.
2.6.1 Le Modèle non contraint
Partant d’abord d’un GARCH (1,1) bivarié pour rendre compte de la problématique se rapportant au nombre de paramètres à estimer pour les GARCH (p, q) multivariés à n composantes. Soient r1,t et r2,t les rendements de deux actifs 1 et 2 obéissants aux processus suivants :
Ce qui nous permettra de construire le GARCH(1,1) bivarié :
Rappelons au travers que non contraint signifie que chaque élément de la matrice variance – covariance conditionnelle est généré par le même type de processus GARCH. Dans la littérature économétrique, on utilise souvent le nom VECH pour désigner cette représentation.
Elle nous permet d’extraire les variances et covariances conditionnelles comme suit :
Précisons que h11t, et h22t, ne sont que les variances conditionnelles de nos deux actifs 1 et 2 et enfin h12t, leur covariance conditionnelle.
Il est clair que ce processus GARCH(1,1) bivarié non contraint nécessite l’estimation de 21 paramètres. Pour un modèle GARCH(p,q) multivarié à n équations, le nombre de paramètres à estimer est donné par la formule suivante :
Ainsi pour un GARCH(1,1) multivarié à n = 4 équations le nombre de paramètres à estimer s’élève à 210. On remarque vite qu’il devient très contraignant d’estimer des processus non contraints pour un nombre élevé de titres. D’ailleurs en pratique on se cantonne à des processus GARCH(1,1) bivarié auquel on impose des hypothèses restrictives pour limiter le nombre de paramètres à estimer, ce qui a donné lieu à différentes conceptions économétriques contraintes.
2.6.2 Modèles contraints
Il ne s’agit pas de lister de manière exhaustive toutes les modélisations multivariées incluant des contraintes, mais nous essayons de présenter brièvement les modèles les plus connus qui nous permettent de mieux cerner notre étude.
2.6.3 Modèle Diagonal
C’est aux travaux de Bollerslev, Engle et Wooldridge (1988) que remonte l’un des plus anciens modèles contraints connu sous le nom de GARCH diagonal. Il s’agit concrètement d’une même représentation que le modèle contraint vu précédemment sauf que les éléments hors diagonale des matrices A et B sont nuls c’est-à-dire :
Cette technique permet de contourner le problème du nombre de paramètres à estimer, que nous avons soulevé auparavant. Cependant comme le note Gourieroux (1994) seule une dépendance des termes avec leurs propres valeurs passées est possible. De plus la condition que la matrice variance – covariance soit positive définie n’est pas garantie et encore cette modélisation n’est pas stable par composition de portefeuille.
2.6.4 Le Modèle BEKK-GARCH
Engle et Kroner (1995) ont proposé la spécification suivante désignée sous le nom BEKK. Cette modélisation élimine l’handicap du modèle diagonal en garantissant une variance positive dans un cadre relativement moins contraignant :
où C est une matrice ( N x N) symétrique, A et B sont deux matrices (N x N) de paramètres constants. Si on se limite à la variante bivariée on aura :
2.6.5 Modèles à facteurs
La référence aux travaux de Engle,Ng et Rothschild (1990) nous renseigne que chaque éléments du processus en question est commandé par des processus à facteurs et d’une innovation. Pour simplifier on se limite au cas d’un seul facteur. Ce faisant, le modèle GARCH(1,1) s’exprime comme suit :
Page suivante : 2.7 Spécification empirique
Retour au menu : INTEGRATION FINANCIÈRE ET DIVERSIFICATION INTERNATIONALE