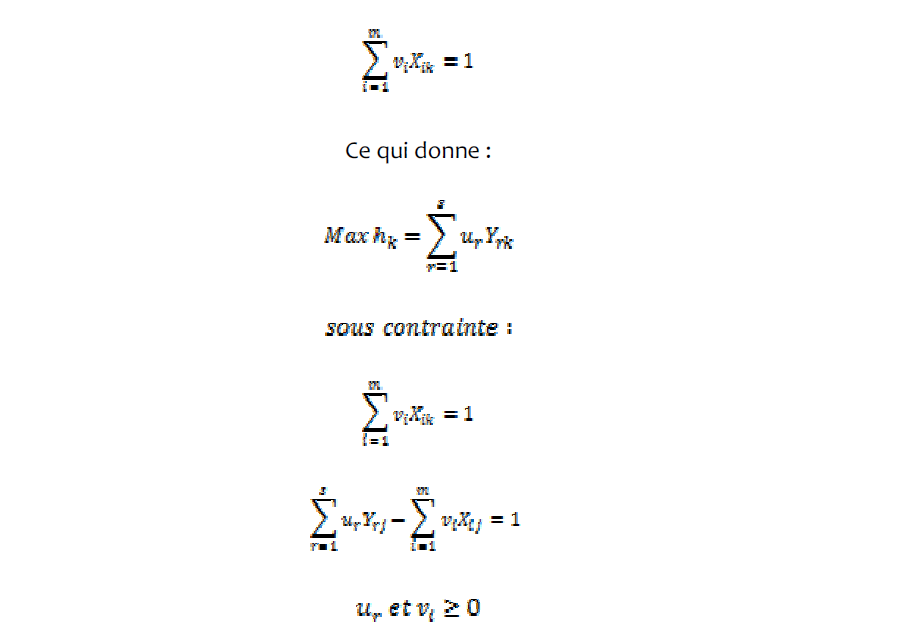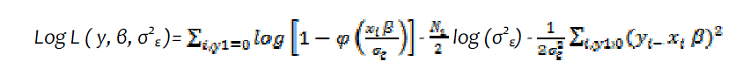En vue d’une analyse pertinente et efficace, nous avons utilisé les méthodes statistiques et économétriques afin d’estimer une fonction de convergence. Etant donné que nous ne disposons pas d’une forme fonctionnelle bien précise (à l’égard de Coob-douglas, CES…), nous faisons donc recours à la méthode non paramétrique qui consiste à estimer une frontière optimale de production. Pour ce qui est de notre, la production n’est rien d’autre que ce niveau de convergence. Dans le cadre de ce travail, l’estimation de cet isoquant optimal passe par la méthode d’enveloppement des données (data enveloppement analysis : DEA). Pour ressortir les écueils à ladite convergence, une analyse basée sur un modèle TOBIT censuré sera effectuée.
Une autre justification est que la méthode DEA permet de réaliser une analyse de l’efficacité à des situations multi produits et de rendements d’échelle non constants.
Elle compare toutes les unités similaires dans une population donnée en prenant en compte simultanément plusieurs dimensions. Il existe donc plusieurs variables dépendantes considérées comme output et plusieurs variables indépendantes considérées comme input. Chaque institution de l’échantillon est considérée comme une unité décisionnelle (Decision-making Unit – DMU) qui transforme des inputs en outputs.
Ainsi, Chaque DMU consomme un montant m de différents inputs afin de produire s différents outputs. Autrement, la DMU (j) (j =1,…m) consomme un montant X {ij} d’inputs (i = 1,…m) et produit un montant Y {rj} d’outputs (r = 1,…s).
Pour arriver à déterminer la frontière d’efficacité technique (niveau de convergence), il nous faut résoudre quelques programmes linéaires. Selon Farell (1957) (cité par KOBOU et al 2009), l’inverse de la fonction distance(35) représente génère des niveaux d’efficacité technique à partir des informations fournies sur les inputs et les outputs. Une ISFD sera efficiente, si elle maximise sa production pour un niveau donné d’inputs. En d’autres termes si son niveau d’efficacité technique est égal à l’unité, c’est-à-dire sa production réalisée est égale à la production optimale. Dans le cas contraire, cette ISFD sera dite moins efficiente et/ou inefficiente.
L’approche CCR développé par Charnes, Cooper et Rhodes en 1978 et adoptée dans ce travail s’aligne dans une logique de rendement d’échelle constant. Cependant, l’hypothèse des rendements constants n’est appropriée que si l’entreprise opère à une échelle optimale (Ambapour, 2001). Ce qui n’est pas toujours le cas (concurrence imparfaite, contraintes financières…). Ce constat a poussé Banker, Charnes et Cooper (1984), à proposer un modèle qui permet d’intégrer l’aspect de rendement variable (BCR).
Ainsi, le modèle CCR peut être modifié en tenant compte de l’hypothèse des rendements variables à l’échelle en ajoutant une contrainte de convexité « N1’λ = 1 » aux programmes distances. Concrètement, il s’agit de maximiser le ratio sommes pondérées des outputs sur la sommes pondérées des inputs.
Cela implique de trouver les valeurs de u et v, de telle sorte que la mesure de l’efficacité de la iième entreprise soit maximisée, sous les contraintes que toutes les mesures d’efficacité soient inférieures ou égales à un. Cependant un problème avec cette formulation particulière en ratio est qu’il existe une infinité de solutions(36). Pour éviter cela, on peut poser :
Cette forme est connue sous le nom de « forme multiplicative » du problème de programmation linéaire. En utilisant le programme dual de la programmation linéaire, on peut dériver une forme équivalente de ce problème d’enveloppement :
– Choix des inputs et outputs
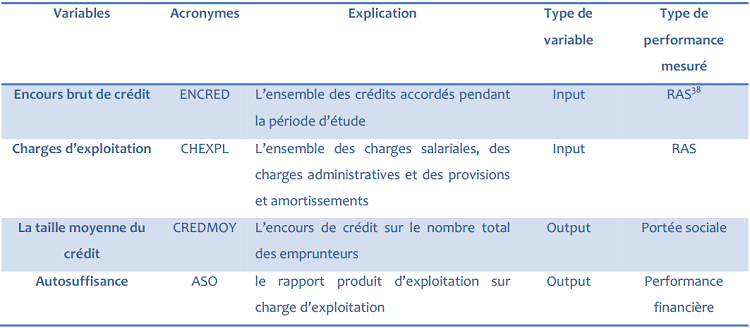
Dans la sélection des inputs, nous n’avons pas voulu s’aligner dans la logique traditionnelle car ce dernier est plus compatible avec les outputs unidirectionnels (mesurer un seul aspect de la performance) car ce travail analyse deux orientations de manière simultanée. S’inspirant de CORNE (2006) et KOBOU et Al (2009), qui ont utilisé le nombre du personnel, le total actif comme input et le ROA et le nombre des femmes emprunteuses comme output. Nous nous sommes démarqués en eux en considérant juste l’actif le plus important, c’est-à-dire l’encours brut de crédit(37) et les charges opérationnelles en lieu et place de l’effectif du personnel. Nos outputs sont orientés dans la performance sociale et dans la portée sociale, ainsi nous avons l’autosuffisance opérationnelle et la taille moyenne de crédit.
Tableau 9 : Les variables inputs et outputs du premier modèle
Source : Analyses auteur
Les DMU(39) qui affichent une valeur de 1 se situent sur l’isoquant d’efficience et réalise ainsi la convergence. Les DMU qui affichent une valeur inférieure à 1 ne sont pas optimaux. La valeur (1 – Efficience du DMU) montre le niveau de l’inefficacité du DMU concerné.
Après l’estimation de l’isoquant représentant le niveau de convergence, un modèle TOBIT censuré sera estimé. Le choix est porté sur un modèle TOBIT censuré car notre variable dépendante (niveau de convergence) sera définie dans un intervalle allant de 0 à 1. (Y € ]0 ; 1]). Cependant, le modèle TOBIT s’applique sous deux contraintes : la variable dépendante est continue dans un intervalle et la probabilité pour que la variable dépendante prenne des valeurs nulles est positive. Concrètement, on observe la variable seulement pour une partie de la population l’autre partie est non observée. Et dans ce dernier cas, on pose sa valeur égale à zéro.
Pour contourner cette contrainte, on expliquera plutôt l’inefficacité (La non convergence) en lieu et place de l’efficacité (la convergence). Ainsi Yi représente le niveau d’inefficacité d’une institution. La partie de l’échantillon constitué des institutions efficaces (convergente) est considérées comme non observée. Le modèle se présente donc comme suit :
Yi* : seuil à partir duquel les variables X affectent l’efficacité des institutions sous études. Dans le cadre de notre étude, la variable dépendante « inefficacité » est continue et limitée à zéro. De plus, les erreurs sont normalement distribuées.
Vu le niveau de biais associé aux estimateurs de la fonction TOBIT par moindre carré ordinaire, et la restriction en une variation binaire astreint par la méthode d’Heckman (Hurlin ), nous faisons recours à l’optimisation de fonction de vraisemblance associées au modèle Tobit afin de ressortir les déterminants de la non convergence. Le modèle de log vraisemblance s’écrit comme suit :
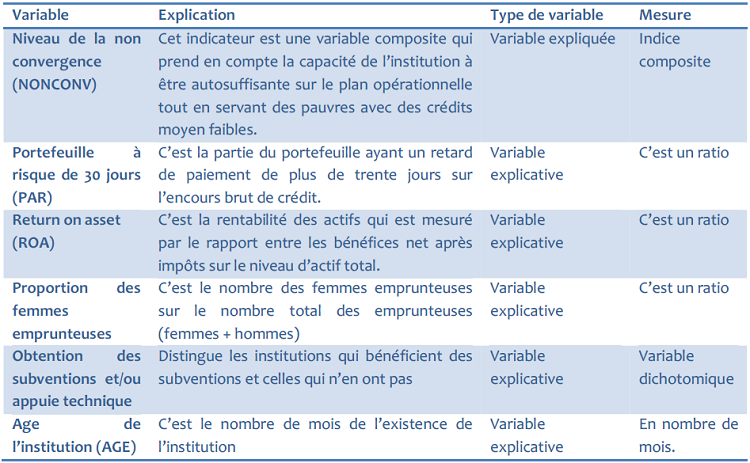
Les variables dépendantes retenues à ce niveau sont les suivantes :
Tableau 10 : La variable endogène et les variables exogènes du second modèle
Source : Analyses Auteur
Après le développement de ce chapitre, il en découle de manière globale que l’industrie de la microfinance à Kinshasa n’est pas encore viable. Par ailleurs, son niveau d’encrage social n’est pas non plus très élevé.
La situation s’accentue avec une analyse basée sur les institutions de notre échantillon. En effet, rare sont les institutions qui maitrise leurs charges opérationnelles et la qualité du portefeuille. Ceci se répercute sur leur niveau d’autosuffisance opérationnelle.
Toutefois, aucune liaison entre les éléments de la portée sociale et les performances sociale n’a été démontrée de manière significative. Du reste, les analyses bi-variées ont de présumait la possibilité d’une convergence entre l’autosuffisance opérationnelle et la portée sociale.
35 La fonction distance est une fonction qui établit une relation entre la production observée et la production optimale.ca permet de cerner le niveau de l’efficacité des DMU sous études. En d’autres termes, elle détermine l’efficacité technique des DMU sous études.
36 En effet, si (u* , v*) est une solution, alors (au* , av*)
37 Il représente près de 80% dans les institutions professionnelles et est générateurs de recettes.
38 Rien à signaler
39 Decision makin unit ou unité décisionnelle en français qui ne représentent les coopératives sous études
Page suivante : Chapitre 3 : Analyse critique et ébauche des solutions