Détection des données aberrantes
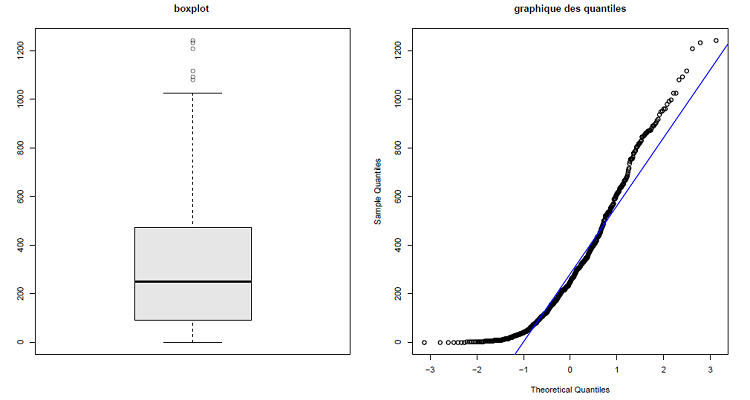
Comme précédemment nous avons utilisé les méthodes graphiques pour la détection des données aberrantes, il s’agit de la boîte à moustache et du graphique des quantiles (figure 3.10). De ces graphes, il en ressort six valeurs aberrantes, ces valeurs sont comprises entre 1000.0 mm et 1240.0 mm. Ces valeurs ne peuvent être considéré comme fausses car il s’agit des valeurs extrêmes de l’échantillon (pics des cumuls mensuels de précipitations observées sur 46 ans). Ces données n’ont pas de corrélation avec le temps (r =-0.06).
Figure 3.10 La boîte à mostache (à gauche) et le graphique des quantiles (à droite) pour la détection des données aberrantes.
– Analyse descriptive
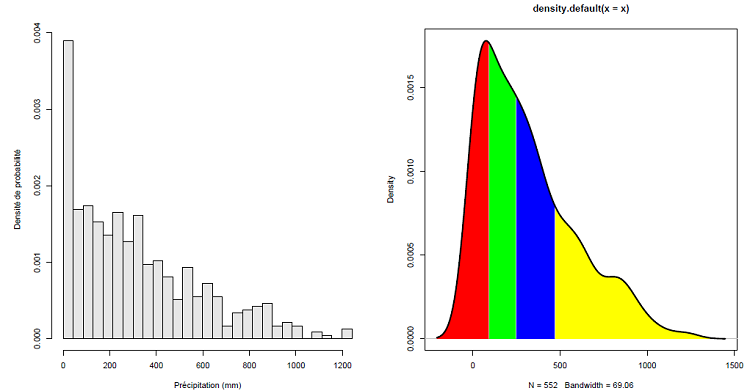
Les résultats de l’analyse descriptive sont consignés dans le tableau 3.7. Il s’agit de la taille des données, les cinq quartiles (minimum, premier quartile, médiane, troisième quartile et le maximum), de la moyenne, de l’écart-type, des coefficients d’asymétrie et d’aplatissement. L’histogramme des données et la courbe de densité représentative des cinq quartiles sont représentés par la figure 3.11.
Table 3.8 Résultats de l’analyse descriptive des cumuls mensuels de précipitations à Douala période 1960-2005
Figure 3.11 Histogramme de la distribution des cumuls mensuels de précipitations (à gauche) et la courbe de la densité de probabilité de la distribution représentatif des cinq quartiles (à droite)
Les coefficients d’asymétrie étant positif, alors la distribution des cumuls mensuels des précipitations est étalée vers la droite et le coefficient d’aplatissement inférieur à 3, ce qui signifie une faible concentration autour de la moyenne. La distribution des cumuls mensuels des précipitations dévie donc fortement de celle de la distribution normale (figure 3.11). Le minimum et le maximum sont respectivement 0.0 mm et 1240.0 mm. Ils sont situés au niveau des queues de distribution, c’est-à-dire des parties extrêmes de la courbe de densité (figure 3.11 . queue gauche (couleur rouge) pour la valeur minimale et droite pour la valeur maximale (couleur jaune)), ces valeurs surviennent avec des probabilités très faibles, elles peuvent donc être considérées comme extrêmes.
3.2.1 Modélisation par la méthode des Maxima par Blocs
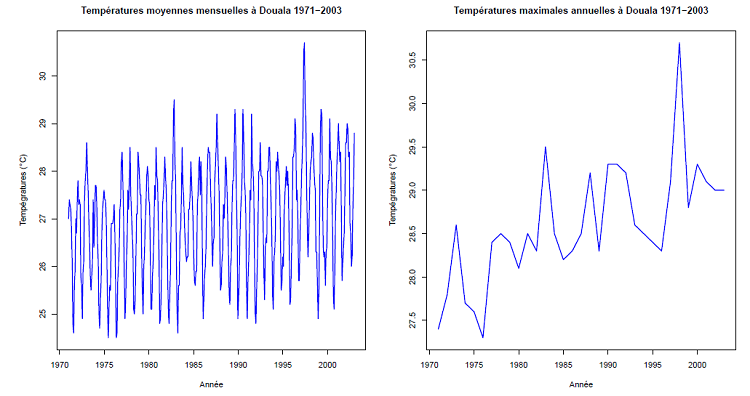
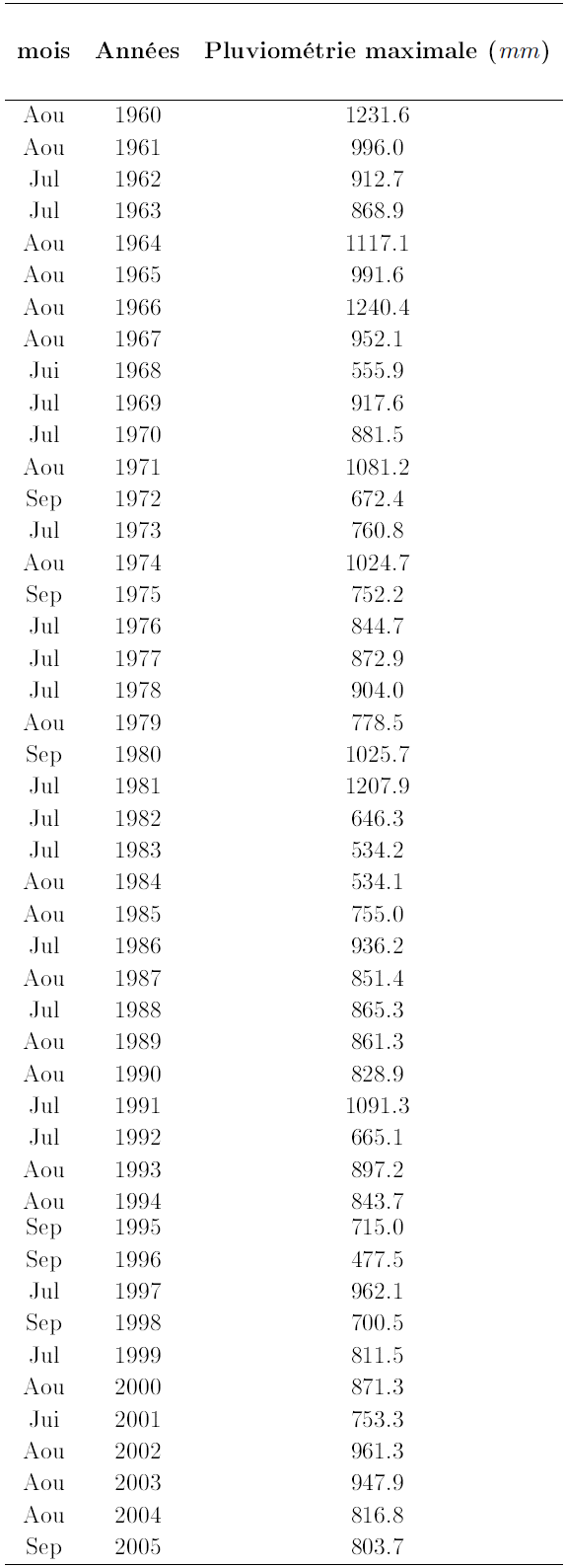
Le choix de la taille des blocs constitue la phase préliminaire de la mise en application de ce modèle. L’échantillon mis à notre disposition étant de taille N=522 et constitué de données mensuelles, nous ferons un regroupement par blocs de 12 mois (taille des blocs k=12), soit un nombre de bloc n=46 et la relation N=nk est ainsi vérifiée. Le choix de taille des blocs étant réalisé, nous pouvons alors constituer un échantillon des maxima annuels des cumuls mensuels de précipitations à partir des données précédentes (cumuls mensuels des précipitations sur 46 ans). L’échantillon ainsi constitué est un échantillon de cumuls des maxima annuels issus des observations mensuelles à Douala de 1960 à 2005 (voir tableau 3.9 et figure 3.12).
Figure 3.12 Distribution des cumuls mensuels (gauche) et des maximums annuels (droite) de précipitations à Douala 1960-2005
Nous avons ainsi constitué un échantillon de 46 pics annuels de cumuls mensuels de précipitations dont les valeurs les plus élevées sont respectivement 1240.4 mm (Août 1966), 1231.6 mm (Août 1960), 1091.3 mm (Juillet 1991), 1081.2 mm (Août1971) et 1025.7 mm (septembre 1980). Ces valeurs correspondent probablement à de graves inondations enregistrées à Douala durant ces années.
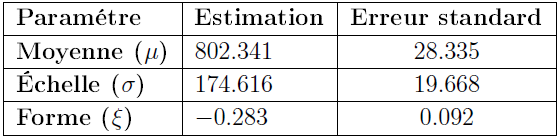
Les paramètres du modèle ont été estimés par la méthode du maximum de vraisemblance. Les résultats sont reportés dans le tableau 3.8. Nous avons obtenu un paramètre de forme négatif (ɛ=-0.283 -/+ 0.092), ce qui signifie que la distribution des valeurs maximales est celle d’une distribution de weibull (voir courbe de densité figure 3.13 et l’équation 3.6 Annexe II).
Table 3.10 Pluviométrie maximales annuelles issues des cumuls mensuels à Douala période 1960-2005
Table 3.11 Paramétres de GEV estimés à partir de l’ajustement des maxima annuels des cumuls mensuels de précipitation à Douala 1960-2005
Les diagnostiques d’ajustement à une loi de GEV des pics annuels est donné à la figure 3.13. Les courbes de probabilité, de quantile et de densité (figure 3.13), montrent que les ajustements obtenus sont acceptables, puisque les nuages de points suivent la courbe théorique (figure 3.13). Ce qui confirme le caractère raisonnable du choix de notre modèle.
Figure 3.13 Méthode des maxima par blocs (BM) . Tracé du diagnostic d’ajustement des maximums annuels des cumuls mensuel de précipitation à Douala, à une distribution de GEV. Du haut à gauche, en bas à droite il s’agit de la courbe des probabilités, des quantiles, des niveaux de retour et de l’histogramme avec un ajustement à une densité de GEV.
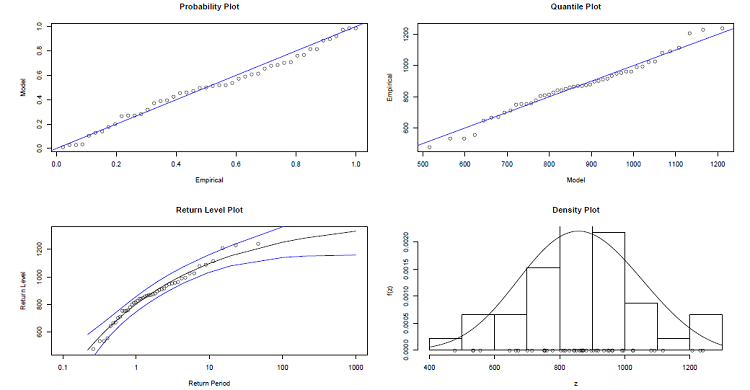
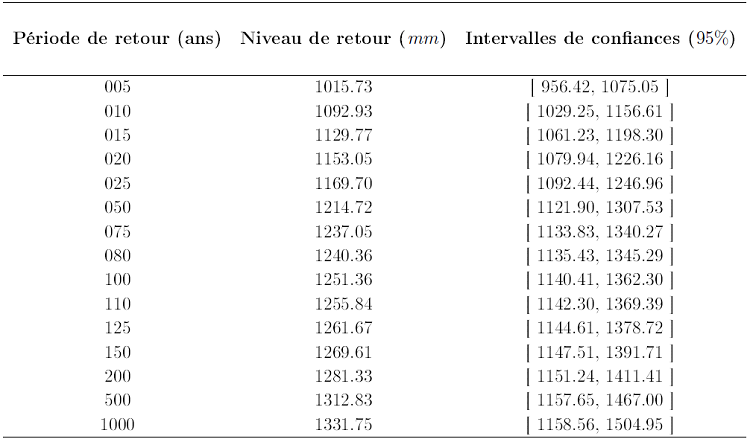
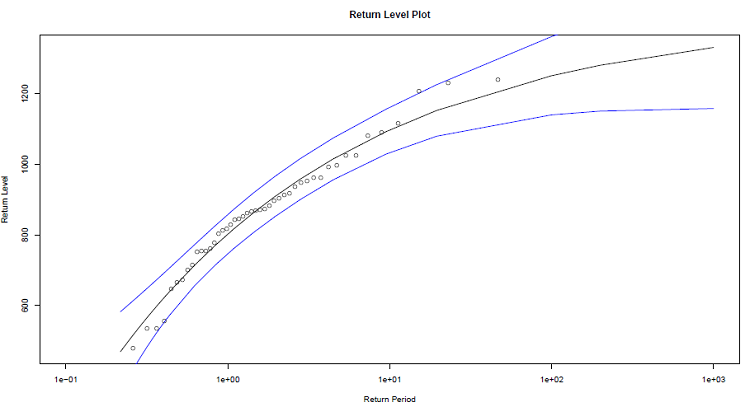
Les résultats du calcul des niveaux de retour (pluviométries extrêmes) auxquels sont associés les intervalles de confiance calculés par la méthode Delta pour différentes périodes de retour ont été reportés dans le tableau 3.10. La courbe de niveaux de retour est représentée par la figure 3.14. Nous remarquons que les valeurs empiriques suivent le modèle GEV. De même les niveaux de retour pour les valeurs maximales des cumuls mensuels de précipitations augmentent graduellement pour des longues périodes de retour.
Table 3.12 Niveaux de retour estimés et intervalles de confiances à 95% calculés par la méthode Delta pour différentes périodes de retour à partir de l’ajustement des maximums annuels de cumuls mensuels de précipitations à Douala à une distribution de GEV.
Figure 3.14 Graphe des niveaux de retour pour les maximums annuels des cumuls mensuels de précipitations à Douala, calculés à partir de la distribution de GEV (courbe en trait noir) avec des intervalles de confiances (courbes en traits bleus) à 95% calculées par la méthode Delta.
Le caractère particulier de l’avènement d’une pluviométrie extrême étant le fait qu’elle est à l’origine de graves inondations. Il est possible avec les résultats précédents d’estimer les intensités de probables niveaux de retour de ces événements extrêmes dans 5, 10, 25, 50, voir même 100 ans et plus. Nous pouvons ainsi estimer la période de retour associée au pic de 1240.40 mm observé en Août 1966. Elle serait de l’ordre 80 ans, c’est-à-dire en Août de l’an 2046.
3.2.2 Modélisation par la méthode de dépassement de seuil
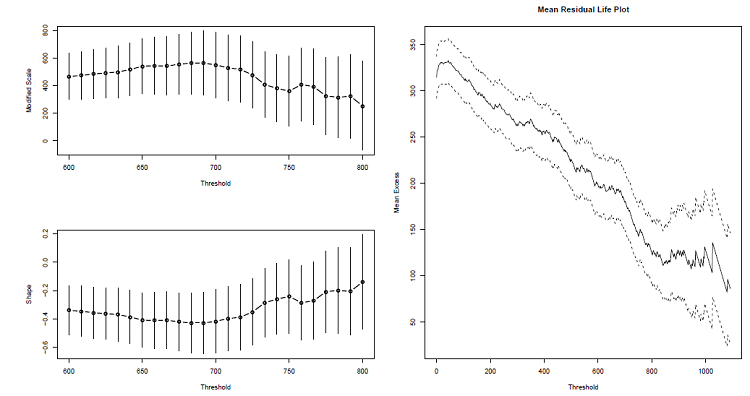
Nous nous intéressons ici à l’échantillon entier de taille N = 552 (cumuls mensuels de précipitations à Douala période 1960-2005), caractérisée par 12 observations mensuelles par ans. Le choix du seuil est l’un des points culminant de la mise en œuvre du modèle. Pour cette sélection du seuil, nous avons appliqué les mêmes techniques que celles appliquées aux températures moyennes. Il s’agit de la fonction moyenne des excès et des graphes des paramètres d’échelle et de forme en fonction des différents seuils, comme l’illustre la figure 3.15.
Figure 3.15 Graphes des paramètres d’échelle et de forme en fonction des différents seuils (courbes gauche) et la fonction moyenne des excès (courbe droite) pour la détermination du seuil, le seul retenu ici est u = 730 mm.
Le seuil retenu ici est u = 730 mm, ce qui conduit à un nombre de valeurs extrêmes égale à 57. L’estimation des paramètres du modèle a été réalisée en utilisant la méthode du maximum de vraisemblance et les résultats sont consignés dans le tableau 3.11.Le paramètre de forme étant négatif (ɛ=-0.304 -/+ 0.121), ce qui signifie que pour ce modèle, la distribution des cumuls mensuels des précipitations au-dessus du seuil u = 730 mm converge vers une distribution de Beta bornée (Équation 3.13 Annexe II).
Table 3.13 Paramètres de la loi GPD estimés à partir de l’ajustement à une loi GPD des températures moyennes mensuelles à Douala, auxquels sont associées le seuil et le nombre d’excès
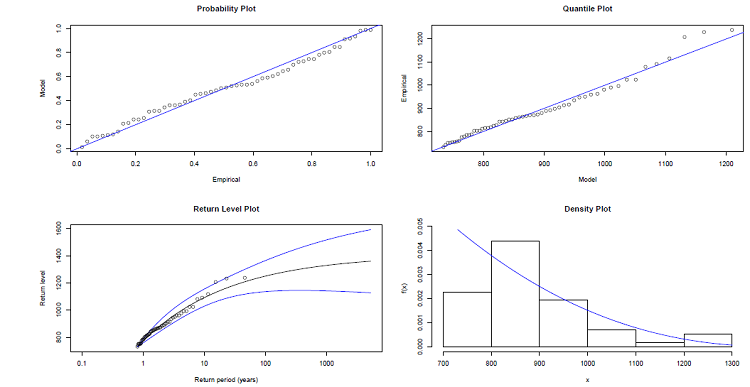
Nous pouvons passer à l’ajustement des données au-dessus du seuil à une loi de GPD. Les graphiques d’ajustement des données à une loi de GPD au-dessus du seuil choisi ci-dessus est données par la figure 3.16. Des graphes de probabilité, de quantile et de densité (figure 3.16), nous pouvons dire que les ajustements obtenus sont acceptable, puisque les nuages de points suivent la courbe théorique (figure 3.16)..
Figure 3.16 Méthode de dépassement de seuil (POT) . Tracé du diagnostic d’ajustement des cumuls mensuels de précipitation à Douala à une distribution de GPD au-dessus d’un seuil (u = 730 mm). Du haut à gauche en bas à droite il s’agit de la courbe des probabilités, des quantiles, du niveau de retour et de l’histogramme avec un ajustement à une densité de GPD.
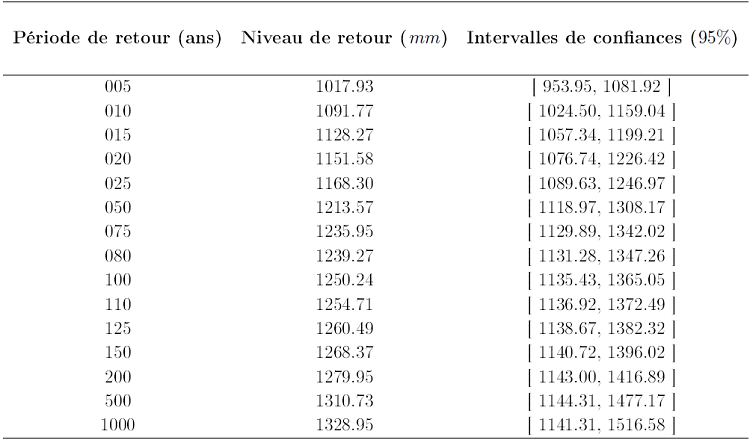
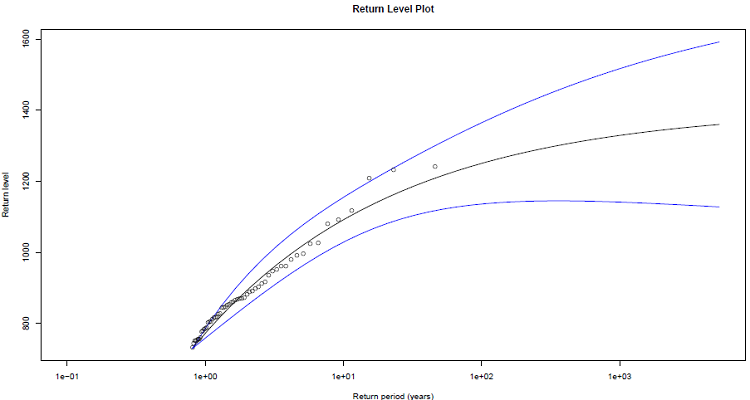
Les niveaux de retour ont été estimés et les intervalles de confiances calculées par les méthodes Delta. Les résultats sont consignés dans le tableau 3.12 et la courbe des niveaux de retour en fonction des périodes de retour est représentée par la figure 3.17. On remarque que les valeurs empiriques suivent le modèle et que les niveaux de retour estimés pour différentes périodes de retour augmentent graduellement pour de longues périodes de retour. Le pic du cumul de précipitation de 1240.40 mm observé en Août 1966, a une période retour de l’ordre de 80 ans.
Table 3.14 Niveaux de retour estimés et intervalles de confiances à 95% calculés par la méthode Delta pour différentes périodes de retour à partir de l’ajustement des cumuls mensuels de précipitations à Douala à la distribution de GPD
Figure 3.17 Graphe des niveaux de retour des cumuls mensuels des précipitations extrêmes à Douala, calculés à partir de la distribution de GPD (courbe en trait noir) avec des intervalles de confiances à 95% (courbes bleues), calculées par la méthode Delta.
3.2.3 Comparaison des résultats issus des deux modèles et Discussions . Cas des cumuls mensuels des précipitations à Douala 1960-2005
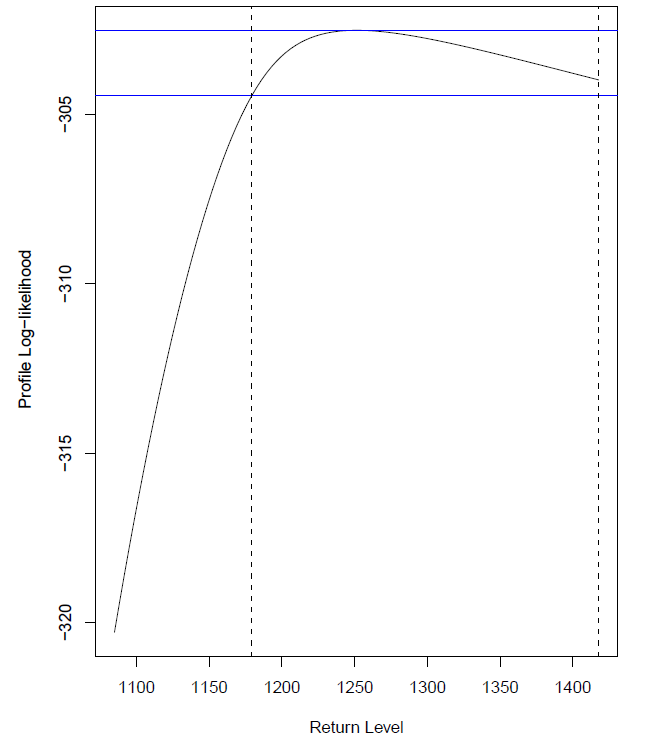
Les valeurs estimées du paramètre de forme sont proches pour les deux modèles, ce qui indique une bonne cohérence entre les deux méthodes. Nous avons obtenu les loi bornées (Weibull et Beta) pour les deux méthodes. L’approche POT conduit à des ajustements légèrement meilleurs que la méthode des maxima annuels, dès lors que l’on choisit un seuil adapté. Les niveaux de retour estimé par les deux méthodes sont proches, notamment ceux du modèle GEV sont légèrement supérieur à ceux du modèle POT (différence comprise entre 1.09 mm et 2.80 mm). Cette différence est aussi observée au niveau des intervalles de confiances. Les intervalles de confiances calculés par la méthode Delta pour les deux modèles sont asymétriques pour de longues périodes de retour, contrairement aux prévisions théoriques. Il serait judicieux d’utiliser le prola vraisemblance. Par exemple le niveau de retour centennale (100 ans) des cumuls mensuels de précipitations extrêmes est 1251.36 mm pour le modèle BM et de 1250.24 mm pour le modèle POT, auxquels sont associés les intervalles de confiances respectives [1179.45; 1417.77] et [1145.02; 1498.60] déterminés en utilisant le prol de vraisemblance (voir figure 3.18 pour le modèle GEV).
Figure 3.18 Le profil de vraisemblance profil pour la détermination de l’intervalle de confiance associé au niveau de retour centennale (1251.36 mm) du cumul mensuel de précipitations extrêmes par le modèles des maxima par blocs (GEV )
Page suivante : Conclusion et perspectives
Retour au menu : Etude des Evénements Extrêmes : cas des Températures et Précipitations à Douala