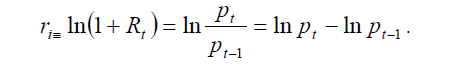Après avoir exploré l’état d’intégration des marchés financiers, nous passons maintenant à l’application empirique du modèle BEKK GARCH multivarié asymétrique. Pour l’élaboration de cette partie nous nous sommes inspiré de la méthodologie adopté par les travaux de Engle et Kroner (1995) et Arouri Mohamed El Hedi (2003). Cette partie constitue l’épine dorsale de ce travail.
3.2.1 Les données et leurs caractéristiques statistiques
Les données utilisées dans cette partie sont celles de six marchés nationaux et un indice du marché mondial. Les six marchés nationaux comportent quatre marchés développés qui sont : la France, la Grande Bretagne, Le Japon et les Etats-Unis et deux pays émergents à savoir : Le Hong Kong et le Singapour. Ces marchés représentent plus de 67% de la capitalisation mondiale. Nous avons puisé les indices MSCI à fréquence mensuelle de Datastream international, le choix d’utilisé des fréquences mensuelles se justifie par la volonté de garder une certaine cohérence avec les autres études et par la disponibilité des données économiques, cette périodicité permet, comme le suggère Harvey (1995) d’éviter certains biais statistiques potentiels. Plus encore, l’utilisation des données mensuelles permet de réduire les biais liés aux transactions non synchronisées et aux discontinuités dans les sessions de transactions qui surviennent sur certains marchés émergents. Notre analyse est faite du point de vue d’un investisseur américain dont l’essentiel des investissements est fait sur le marché intérieur. Ce faisant, nos séries de rendements sont exprimés en dollars américains pour fins de comparabilité.
Ce faisant, nous poserons implicitement comme hypothèse, que les investisseurs ne couvrent pas leurs positions face aux fluctuations du taux de change.
Nos rendements boursiers sont donc calculés mensuellement à partir de Datasteam international et couvrent la période de janvier 1973 à décembre 2007. Comme à l’accoutumée, chaque séries des indices boursiers a été transformée en séries de rendement continuellement composés ri en prenant la différence du logarithme des prix :
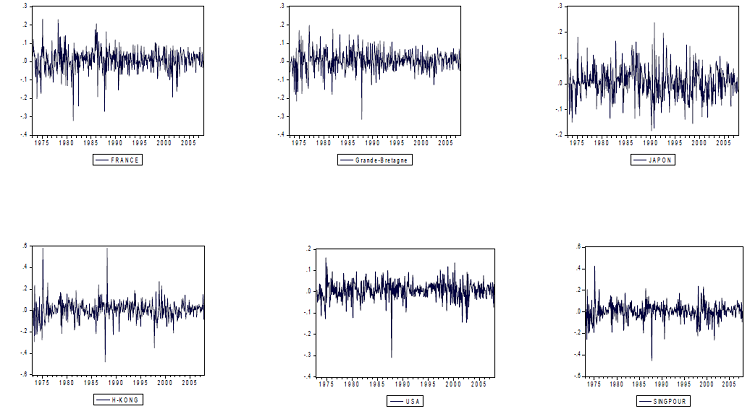
Le fait de travailler avec les rendements à comme impact de rendre la série stationnaire, comme on peut le constater de visu en faisant une comparaison entre les figures ci-dessous :
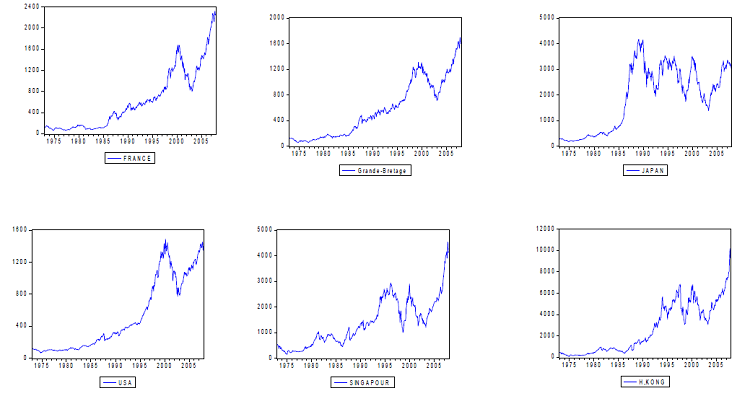
Figure 5 : Indices boursiers mensuels
Figure 6 : Rendements boursiers mensuels
On constate à la figure 5 que l’indice japonais à une allure différente de celle des autres pays. En effet, de 1990 environ à 2007, aucune tendance ne semble se détacher de la série, celle-ci atteignant une sorte de plateforme. Étant donné que cette tranche représente plus de la moitié de l’échantillon, cela pourrait s’avérer un élément important au niveau des tests de normalité qui seront effectués. De plus, on constate que le marché japonais a connu une croissance spectaculaire parmi tous les pays, toutes les époques confondues, sans indices passant d’environ 1000 à 4500 au cours de la période 1985-1989.
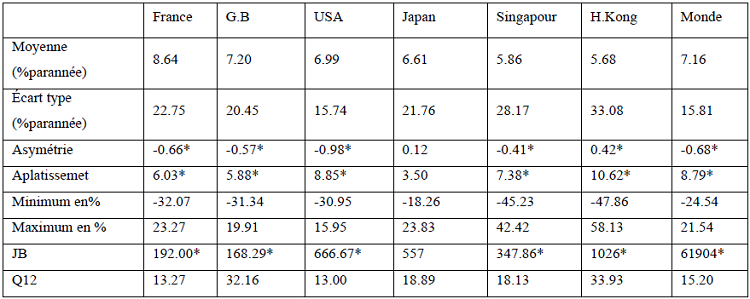
Tableau 5 : récapitulatif des statistiques descriptives des rendements
* significatif au seuil de 1%
** significatif au seuil de 5%
*** significatif au seuil de 10%
JB. test de normalité de Jaque-Bera
Q(12) : test de Ljung-Box d’ordre 12
La lecture de ce tableau nous renseigne que les coefficients d’asymétrie sont majoritairement significativement négatifs, la distribution des séries est étalée vers la gauche, ce qui prouve que, dans la plupart du temps, l’effet d’un choc négatif est plus important que celui d’un choc positif. On remarque aussi le caractère leptokurtique des séries de rendements car le coefficient d’aplatissement centré est supérieur à trois pour toutes les séries. L’aplatissement excédentaire témoigne d’une forte occurrence des points extrêmes, donc une distribution à queues épaisses. En définitive, exception faite du Japon, l’hypothèse de la normalité est rejetée pour tous les marchés nationaux y compris le marché mondial comme l’illustre le test de Jaque et Berra. Ceci nous conforte dans l’estimation d’un modèle non linéaire et plus particulièrement d’un modèle de type GARCH multivarié asymétrique présenté plus haut qui permet de capter ces propriétés.
En scrutant aussi ce tableau, il est manifeste que la France a le rendement mensuel moyen le plus important, Hong Kong a le score le plus bas. En terme de volatilité ce sont les États-Unis qui sont le marché le moins volatil ce qui pourrait s’expliquer par le fait que les rentabilités sont toutes converties en dollar américain et par conséquent la variance non conditionnelle n’inclue pas pour le cas américain le risque de change. Sans surprise, les marchés les plus volatils sont les deux marchés émergents à savoir : Singapour et Hong Kong.
Le test de Ljung-Box nous confirme l’absence d’autocorrélation sérielle pour tous les indices financiers, raison pour laquelle l’inclusion d’un ajustement autorégressif (AR) dans le processus régissant la moyenne ne s’impose pas.
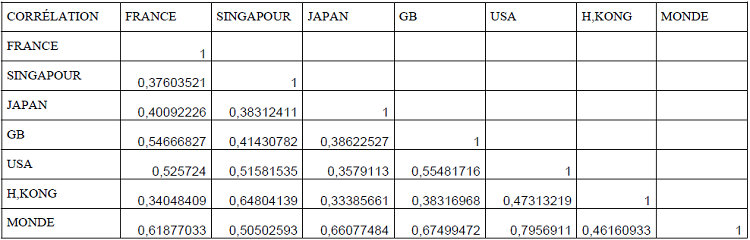
Le tableau 2 quant à lui nous éclaire sur les corrélations des rendements des différents marchés étudiés et l’indice mondial.
Tableau 6 : Corrélations des rentabilités
Ce tableau nous indique que les marchés industrialisés occidentaux et le Japon sont fortement corrélés avec l’indice mondial comme le témoigne la dernière ligne. Sans surprise la corrélation la plus consistante avec l’indice mondial est celle des Etats-Unis qui s’élève à presque 80%. H.Kong présente une corrélation de 64% avec le Singapour.
L’analyse de ces corrélations inconditionnelles suggère a priori que l’intérêt de la stratégie de la diversification demeure alléchant de point de vue de l’optimisation du rapport rendement risque.
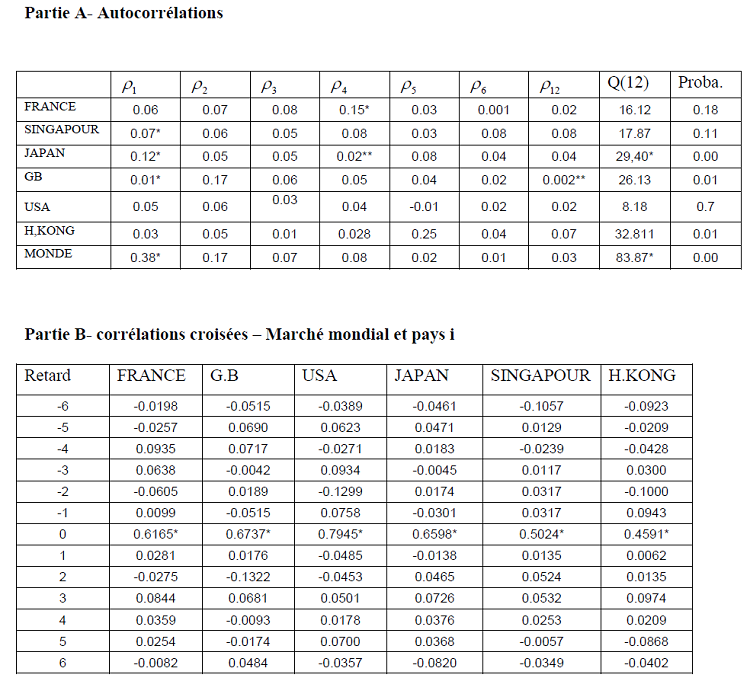
Nous savons, d’autre part, que le processus GARCH (1,1) est le mieux adaptable pour la modélisation des séries financières. Ceci est un fait stylisé très bien documenté dans la littérature empirique de Bollerslev (1986), Pour nous en convaincre, nous établirons dans le tableau 7 les autocorrélations et les corrélations croisées des carrés des excès de rentabilités.
Tableau 7 : Autocorrélations et corrélations croisées des excès de rentabilités
*significatif au seuil de 1%
** significatif au seuil de 5%
*** significatif au seuil de 10%
JB. test de normalité de Jaque-Bera
Q(12) :test de Ljung-Box d’ordre 12
Du tableau 7 on remarque que sur sept séries il y a quatre dont les autocorrections d’ordre un des carrés des rendements excédentaires sur le taux sans risque des rendements sont significatives ce qui laisse supposer qu’il s’agit d’un processus GARCH d’ordre 1. Les corrélations croisées quant à elles laissent comprendre que seules les corrélations synchrones c’est dire correspondant à la ligne du retard 0 sont consistantes et significatives. Ce constat, montre que pour nos séries à fréquence mensuelles les dépendances en terme de volatilité ne sont pas significatives ce qui milite en faveur de la diagonalité des matrices A,B, S et T dans la matrices des variances–covariances.
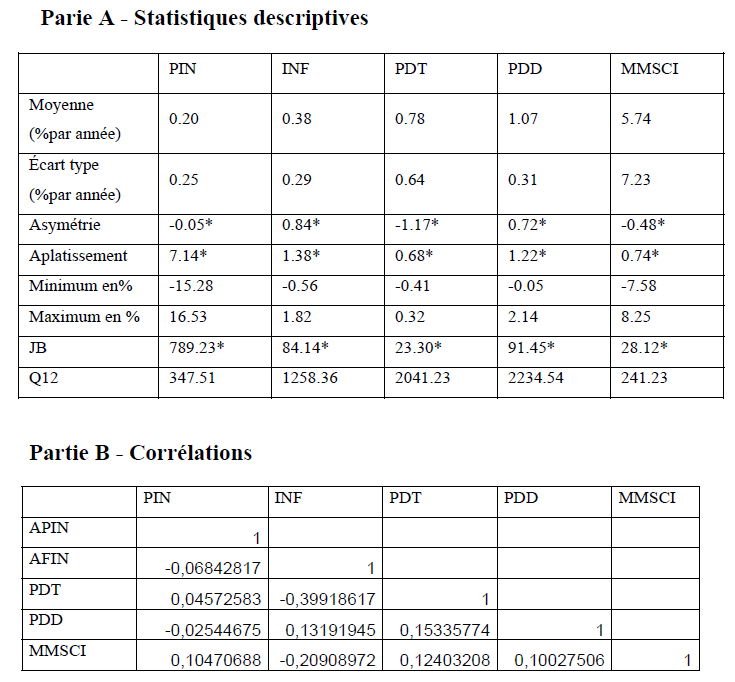
Tableau 8 : Statistiques descriptives et corrélations des variables économiques
*significatif au seuil de 1%
** significatif au seuil de 5%
*** significatif au seuil de 10%
JB. test de normalité de Jaque-Bera
Q(12) :test de Ljung-Box d’ordre 12
À l’analyse, les corrélations entres les variables macroéconomiques sont relativement faibles. Il semble que le vecteur informationnel Z ne contient pas de redondances.
Page suivante : 3.3 Mise en application du modèle
Retour au menu : INTEGRATION FINANCIÈRE ET DIVERSIFICATION INTERNATIONALE