En vue d’étudier la stationnarité des deux séries, nous allons réaliser le test de
Dickey-Fuller Augmenté (ADF). Ce test à été développé en 1981 en se basant sur
l’hypothèse de corrélation des résidus et et sur l’estimation par la méthode des moindres
carrés ordinaires (MCO) des 3 modèles suivants :
Sachant que les résidus (et) sont indépendamment et identiquement distribués (iid).
3.2.2.1. Test de stationnarité de la série de prix
Tableau 1.3 : test de stationnarité de la série des prix : modèle avec tendance et constante « en niveau »
Selon le tableau 1.3, il est possible de constater que la tendance n’est pas significative,
puisqu’elle présente une erreur de 9,11% qui est supérieure au seuil tolérable de 5%. Il en
résulte que le modèle approprié pour tester la stationnarité de la série des prix est celui qui
ne présente pas de tendance. Par conséquent il convient de passer à la deuxième étape.
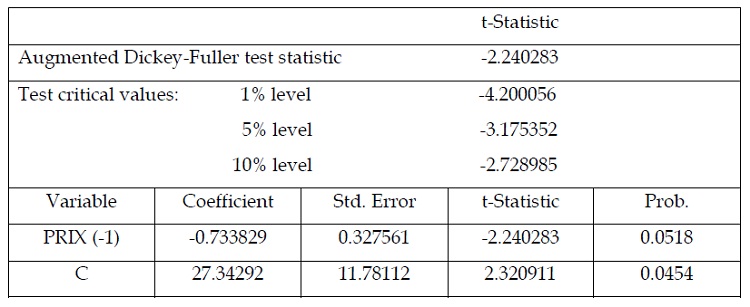
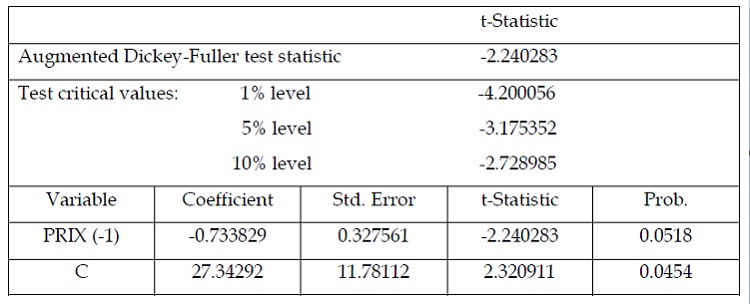
Tableau 1.4 : test de stationnarité de la série des prix : modèle avec constante « en niveau »
D’après ce tableau, il est possible de constater que la constante est significative du
fait qu’elle est égale à 4,54% qui est inférieur au seuil tolérable de 5%. Il en résulte que le
modèle avec constante semble être le plus approprié pour tester la stationnarité de la série
des prix. Cependant l’application du test Augmented Dickey Fuller (ADF) sur la série des
prix, fait ressortir la présence d’une racine unitaire dans la série en niveau, donc la série est
non stationnaire du fait que la statistique ADF qui égale à(-2,240283) est supérieure à la
valeur critique au seuil de 5% qui égale à ( -3,175352). D’où la nécessité de passer à l’étape
suivante qui consiste à appliquer le test ADF sur la série en différence première dont le
but est de tester l’ordre d’intégration de la série.
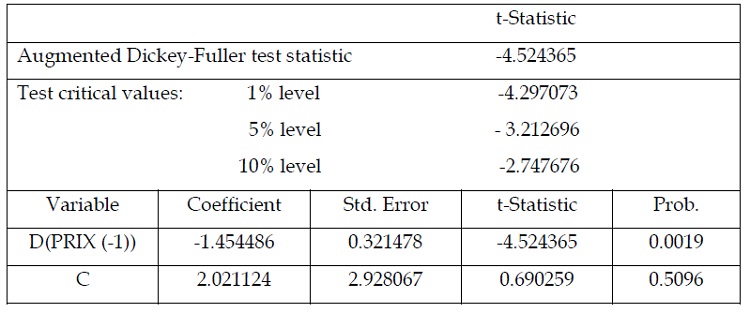
Tableau 1.5: test de stationnarité de la série des prix : modèle avec constante « en différence première »
Il en découle du tableau 1.5 que la série des prix est stationnaire en différence
première et ce étant donné que la statistique ADF qui égale à (-4,524365) est inférieure à la
valeur critique au seuil de 5% qui égal à (-3,212696).
Après avoir établit toutes les étapes nous pouvons conclure que notre série des prix
est stationnaire en différence première uniquement avec constante.
3.2.2.2. Tests de stationnarité de la série des dividendes :
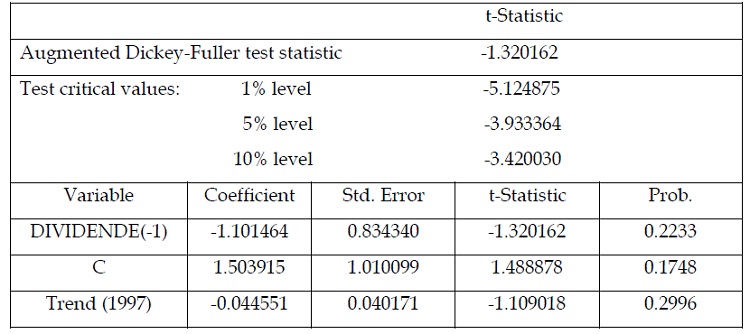
Tableau 1.6: test de stationnarité de la série des dividendes : modèle avec tendance et constante « en niveau »
Nous remarquons à partir du tableau 1.6 que la tendance n’est pas significative,
puisqu’elle présente une erreur de 29,96% largement supérieure au seuil tolérable de 5%.
Par conséquent, le modèle approprié pour tester la stationnarité de la série des dividendes
est celui qui ne présente pas de tendance, d’où le recours à la deuxième étape.
Tableau 1.7 : test de stationnarité de la série des dividendes : modèle avec constante « en niveau »
Le tableau 1.7 fait ressortir que la constante n’est pas significative du fait qu’elle est
égale à 18,78% qui excède largement le seuil tolérable de 5%. Donc, il en résulte que le
modèle le plus approprié pour tester la stationnarité de la série des dividendes est celui
qui ne présente ni tendance ni constante.
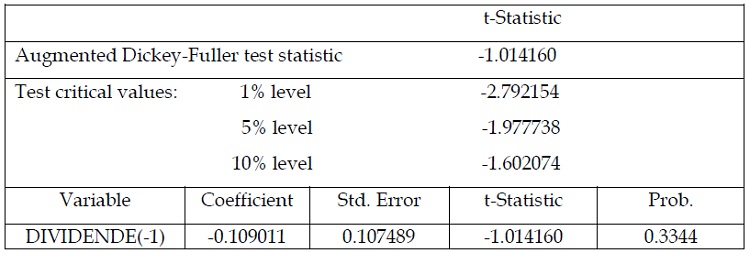
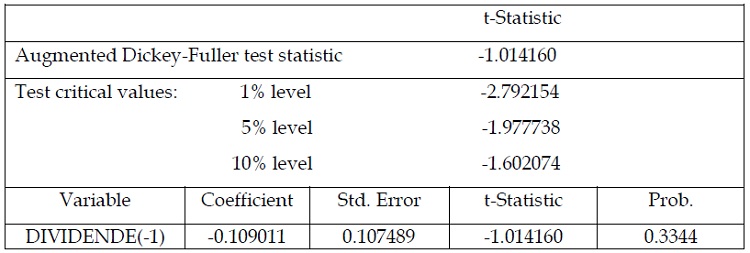
Tableau 1.8 : test de stationnarité de la série des dividendes : modèle sans tendance ni constante « en niveau »
Après avoir effectué le test de racine unitaire de Dickey –fuller sur la série des
dividendes, nous avons vu que la série est non stationnaire en niveau et ce car la
statistique ADF qui égale à (-1.0141160) est supérieure à la valeur critique au seuil de 5%
qui égal à (-1.977738). D’où la nécessité d’appliquer le test ADF sur la série en différence
première et ce afin de tester l’ordre d’intégration de la série.
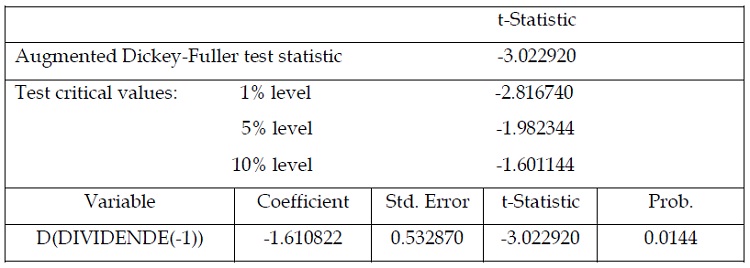
Tableau 1.9: test de stationnarité de la série des dividendes : modèle sans tendance ni constante « en différence première »
Il en découle de ce tableau que la série des dividendes est stationnaire en différence
première et ce étant donné que la statistique ADF qui égale à (-3.022920) est inférieure à la
valeur critique au seuil de 5% qui égal à (-1.982344).
Après avoir établit toutes les étapes nous pouvons conclure que notre série des
dividendes est stationnaire en différence première sans constante ni tendance.