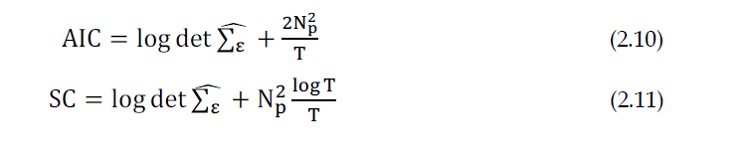Etant donné qu’on à vérifié au préalable la stationnarité et la normalité de la série
des rendements mensuels du marché, nous pouvons ainsi appliquer directement le test de
Box et Jenkins (1976).
Le processus stationnaire (Rt , t E Z) autorégressif moyenne mobile d’ordre (p,
q) ou ARMA (p, q) est définit par la formulation suivante :
(2.9)
Conformément au test de Box et Jenkins, l’étape d’identification du modèle le plus
approprié consiste à déterminer les ordres de retard p et q qui nécessite à son tour le
recours à l’analyse des corrélogrammes des coefficients d’auto corrélation (FAC) et des
coefficients d’auto corrélation partielle(FACP). A cet effet, nous allons estimer les
paramètres des modèles candidats ARMA à l’aide de la méthode des moindres carrés
ordinaires (MCO) qui présente une étape primordiale et obligatoire. Le choix de la
spécification ARMA est réalisé à partir de la méthode des critères d’information, cette
dernière consiste à retenir parmis un certain nombre de modèles estimés pour un nombre
de retards allant de 0 à h ( h est le retard maximal) , celui dont le retard p minimise les
critères d’Akaike (AIC) et Schwartz (SC) définis par :
Où :
N : Le nombre de variables,
T : Le nombre d’observations,
S : Est un estimateur de la matrice variance covariance des résidus.
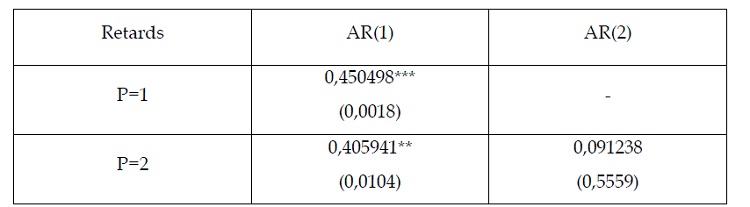
Tableau 2.8 : estimation du processus AR(p) par la méthode MCO
***, **,* : niveaux de significativité respectivement de 1%, 5% et 10%.
L’analyse du tableau ci-dessus nous montre que le processus AR(1) est à retenir.
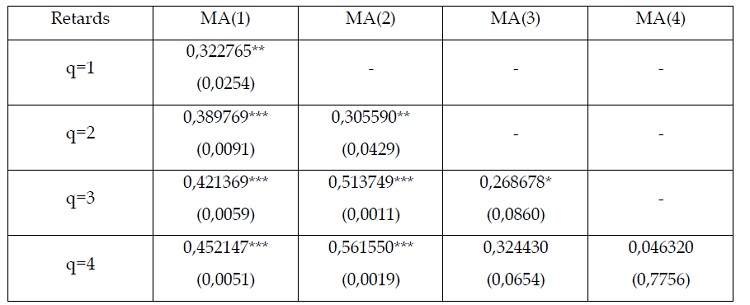
Tableau 2.9 : estimation du processus MA(q) par la méthode MCO
***, **,* : niveaux de significativité respectivement de 1%, 5% et 10%
Le processus à choisir d’après ce tableau MA(3).
A partir des résultats qui ont été fourni par les deux tableaux précédents, nous
constater à priori que le modèle ARMA(1,3) est le modèle estimé par la méthode MCO.
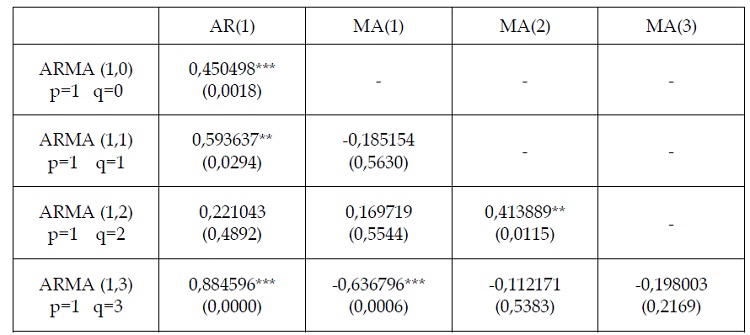
Tableau 2.10 : estimation du processus ARMA (p,q) par la méthode MCO
***, **,* : niveaux de significativité respectivement de 1%, 5% et 10%
Le tableau montre que le processus à retenir est le ARMA(1,0) car le ARMA(1,3) est non
significatif dans les processus MA(2) et MA(3).