L’étude empirique s’est déroulée en deux étapes et évaluera la performance à la lumière de deux indicateurs regroupés sous une batterie de ratios que sont les ratios de rentabilité et de productivité.
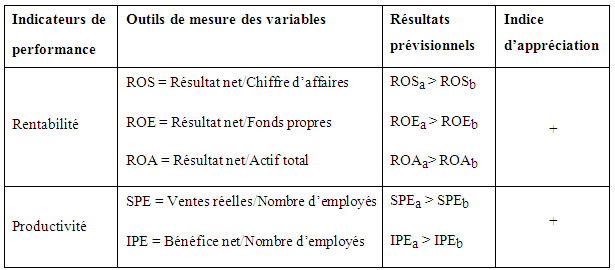
La méthodologie utilisée dans la première étape est inspirée de celle utilisée par Megginson et al. (1994). Elle a permis principalement de tester l’efficacité statique, en évaluant l’incidence de la privatisation sur les deux variables de performance retenue dans cette étude (rentabilité et productivité). En effet, cette étape a consisté d’abord en un simple calcul à partir d’Office Excel 2010 des ratios de rentabilité et de productivité entreprise par entreprise et, en moyenne, sur des périodes de trois années, avant et cinq années après la privatisation, l’année de privatisation étant considérée comme l’année d’origine et donc prenant la valeur O. Ensuite, nous avons comparé la moyenne des ratios avant la privatisation à ceux après la privatisation pour chaque entreprise. Une récapitulation des ratios d’analyse est présentée dans le tableau suivant :
Tableau 5 : Présentation des ratios d’analyse
Source : l’auteur
Légende
ROS : Return On Sales ou taux de marge nette
ROA: Return On Assets ou rentabilité des actifs
ROE : Return On Equity ou rentabilité des capitaux propres
SPE : Sales Per Employee ou productivité commerciale
IPE : Income Per Employee ou bénéfice par employé
L’indice a signifie « after privatization» ou après privatisation
L’indice b signifie « before privatization» ou avant privatisation
Enfin, nous avons fais recours au test de différence de médiane (test de Wilcoxon), afin de mettre en exergue les éventuels changements qui ont prévalu dans la performance des entreprises publiques privatisées et de dire si ces changements sont significatifs.
– Description du test de différence de médiane
Ce test non paramétrique nous permet de cerner l’effet statique de la privatisation sur la performance des huit entreprises publiques camerounaises. De manière plus explicite, quatre étapes permettent de parcourir le test dans le cas où N, le nombre de paire d’observations non nulles est inférieur ou égal à 30.
– Etape 1 : on détermine les différences DI et on les classe dans l’ordre croissant de leur valeur absolue en écartant les différences nulles.
Si nous revenons à notre étude, DI = MOYai – MOYbi
Avec : MOYai, la moyenne du sous échantillon après la privatisation pour l’entreprise i
MOYbi, la moyenne du sous échantillon avant la privatisation pour l’entreprise i
– Etape 2 : on fait la somme des rangs des différences positives qu’on note T+, et celle des différences négatives en valeur absolue notée T-.
– Etape 3 : pour la suite du test, nous prenons la valeur minimale entre T+ et T-. Cette valeur notée T sera utilisée pour prendre notre décision.
– Etape 4 : on décide. On lit dans la table de Wilcoxon, la valeur critique de T correspondant à N et à un seuil de significativité.
Si T est inférieur ou égal à la valeur critique lue sur la table, on rejette l’hypothèse nulle.
En prenant l’exemple de notre première hypothèse : “la privatisation améliorerait la rentabilité des entreprises publiques camerounaises”, nous aurons :
HO : pas de différence entre les situations avant ou après la privatisation. (Dans ce cas notre hypothèse n’est pas vérifiée).
H1 : il y a une différence entre les deux situations. Et particulièrement dans notre étude, cette différence doit être positive pour signifier un accroissement. Il faudrait ainsi que T+ soit supérieur à T-.
Ainsi après lecture dans la table de la valeur critique de T, nous pouvons nous prononcer de la manière suivante :
De façon à mieux rendre compte de la dynamique temporelle, des tests complémentaires (test de Wilcoxon) ont été conduits sur la valeur des mêmes indicateurs (rentabilité et productivité) en opposant successivement les années extrêmes – 3/+ 5, puis – 3/0 (période de pré-privatisation) et, enfin, 0/+ 5 (période de post-privatisation). Cette deuxième variante de la procédure de Megginson et al. (1994) présente deux avantages :
Premièrement, l’effet éventuel de la privatisation risque d’être plus accentué et plus apparent, s’il est évalué en opposant les données des années – 3 et + 5, plutôt qu’à partir des moyennes avant et après privatisation. Les changements de niveaux de performance mettent habituellement un certain temps à apparaître de façon significative à travers les données comptables.
Deuxièmement, cette variante permet de savoir si l’incidence s’est produite avant la privatisation, après la privatisation ou, progressivement, au cours des neuf années d’observation. De cette façon, on peut mettre en évidence, au moins de façon grossière, la dynamique du processus de privatisation. Toujours dans le même objectif, nous avons mesuré ensuite, pour les deux méthodes, le pourcentage d’entreprises pour lequel la variation de l’indicateur a été conforme aux prédictions théoriques, et nous avons testé (test non paramétrique du signe) la significativité de cette proportion. Ce test permet d’échapper aux biais qui entachent les tests effectués sur les moyennes. Cependant, quelque soit la méthode retenue, l’effet dynamique de la privatisation n’est mesuré que très imparfaitement.
Pour répondre à cette critique, nous avons dans une deuxième étape, eu recours à l’aide du logiciel EVIEWS 7 à la procédure proposée par Villalonga (2000) : le modèle économétrique SUR le modèle économétrique SUR (Seemingly Unrelated Regressions)
Il s’agit de mesurer, dans un modèle de régression, les taux d’accroissement de la performance après la privatisation. Pour cela, les principaux indicateurs de performance ont été régressés sur trois variables :
– une première variable, le temps T (les valeurs 1 à 9 désignant les neuf années) ;
– une seconde variable muette P traduisant la privatisation valant 0 quand l’entreprise est publique et 1 lorsqu’elle est privatisée ;
– une troisième et dernière variable, dénommée TP, égale au produit de la variable temps et de la variable muette « privatisation ».
Compte tenu de la double dimension des données, transversale et temporelle, la régression a porté sur 72 observations (8 entreprises sur 9 ans) et se présente sous la forme générale suivante :
PERFit = αi + β1i Tit + β2iPit + β3iTPit + β4 tailleit+ β5 cycleit +εit (1)
Avec :
PERFit : la variable mesurant la performance de l’entreprise i à l’année t
Tit : le temps t pour la firme i (valeurs allant de 1 à 9 pour les neuf ans considérés pour chaque entreprise).
Pit : une variable muette de privatisation qui prend la valeur 1 lorsque l’entreprise i est devenue privatisée et 0 avant la privatisation.
TPit : une variable exprimant l’interaction des deux variables précédentes ;
tailleit : la taille de l’entreprise (mesurée par le chiffre d’affaires) de l’entreprise i à l’année t.
cycleit : le taux de croissance du PIB (Produit Intérieur Brut), l’année t pour la firme i.
En effet, dans son étude, Villalonga (2000) teste dans l’équation (1), l’effet du temps T, de la privatisation P et TP (le produit de la variable temps et de la variable P et qui nous donne la période post privatisation) sur l’efficacité. Il est à noter que le temps T couvre les années d’observation (neuf années) ; la variable P est une variable indicatrice qui prend la valeur 0 lorsque l’entreprise est encore publique et la valeur 1 lorsqu’elle est privatisée. La variable TP est une variable qui traduit l’horizon de temps dans lequel l’entreprise est privatisée. Le coefficient de la variable TP permet de mesurer et de tester l’effet sur l’accroissement de la performance au cours de la privatisation c’est-à-dire sur six années, l’année de privatisation et les cinq années qui suivent pour chacune des entreprises. Les coefficients de la variable P permettent de mesurer et de tester, pour chaque entreprise l’effet seuil de la privatisation.
L’équation (1) suppose que la performance de l’entreprise (exprimée par le ROS, le ROE, le ROA, le SPE et l’IPE) est expliquée par la variable temps (T), la privatisation (P), la période post privatisation (TP), la taille (mesurée par le chiffre d’affaires) et la croissance du produit intérieur brut (cycle).
A l’instar des travaux de Villalonga et Charreaux, l’équation (1) suppose que les effets de la taille et du cycle économique sur la performance sont identiques quelle que soit la firme. A la suite de Villalonga (2000) et de Charreaux (2004), nous faisons ainsi l’hypothèse implicite que les facteurs communs : taille et cycle (9) échappent au contrôle des firmes et qu’il n’y a pas de lien direct entre l’incidence de la privatisation sur la performance (rentabilité et productivité) et la taille. Les effets des variables T, P et TP sont, en revanche, spécifiques à chaque entreprise et sont supposés fixes.
9 De même que Villalonga (2000, p, 58, note 17) et Charreaux et Alexandre (2001, p22, note 21) et pour la même raison inhérente au faible nombre de firmes retenues dans l’échantillon, la constante n’a pas été remplacé par une variable transformée égale à l’écart type par rapport à la moyenne comme c’est le cas lorsqu’on estime les modèles à effets fixes sur des échantillons de grandes tailles.