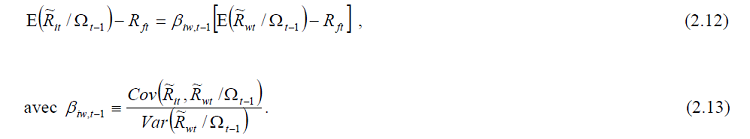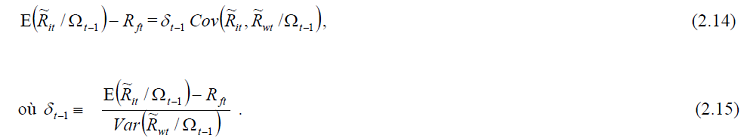Sharpe (1964) a confectionné une variante conditionnelle de MEDAFI s’exprimant comme suit :
βiw,t−1 signifie la réactivité variable selon les dates du titre ou de portefeuille i au du marché mondial W. Les espérances du rendement sont calculées par rapport à l’ensemble des informations −1 Ωt disponible en t-1.
On peut reformuler l’équation (2.12) de telle manière qu’elle constitue un cas particulier du modèle d’Alder et Dumas (1973) :
δt-1 constitue le prix variable dans le temps de la covariance du marché.
La référence à Stulz (1981), Bekaert et Harvey (1995) et De Santis et Gerard (1998) nous montre que la formulation (2.15) est fréquemment employée dans les études empiriques car elle augure que les marchés financiers sont intégrés. Ce faisant, l’homogénéisation des comportements au niveau des marchés financiers impose des prix de risque identiques ou comme l’exprime Arouri Mohamed El Hedi (2003) “Cette formulation suppose implicitement que les marchés financiers sont intégrés, c’est-à-dire le prix de risque de marché est le même pour tous les actifs financiers et pour tous les investisseurs”.
De Santis et Gérard (1998) évoquent l’intérêt de l’équation (2.14) qui permet de quantifier les gains substantiels qui pourraient résulter de la diversification internationale. La version conditionnelle du MEDAFI est outil indispensable pour juger l’impact pratique de l’intégration financière dans la stratégie de la diversification à l’international.
Retour au menu : INTEGRATION FINANCIÈRE ET DIVERSIFICATION INTERNATIONALE