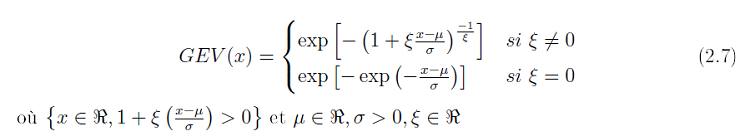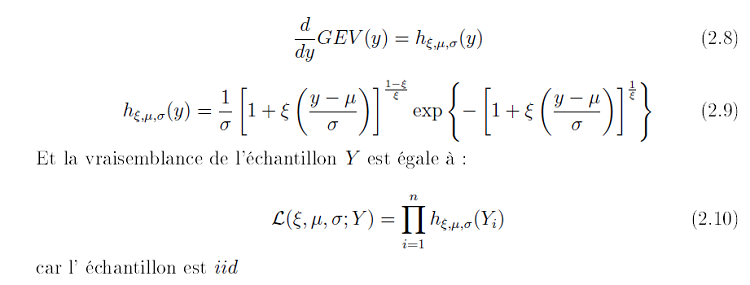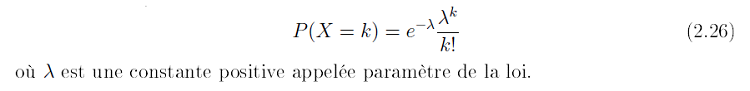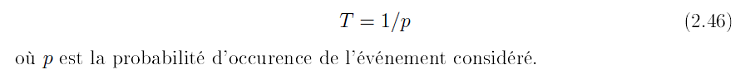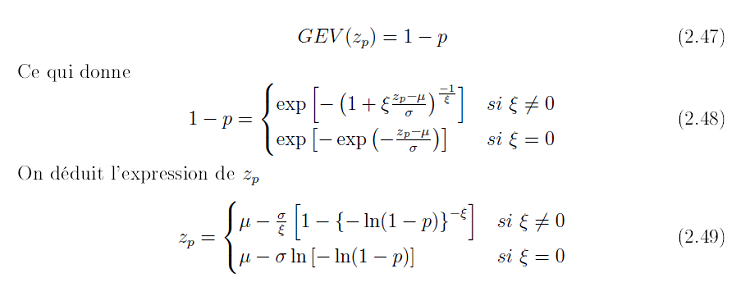Lorsque nous disposons d’un échantillon de données à analyser, notre première préoccupation est celle de savoir si ce dernier est able, c’est-à-dire s’il ne contient pas de fausses mesures. La détection de données aberrantes est d’une première importance pour l’analyse des valeurs extrêmes (maxima et minima d’un échantillon).
Il est donc important de détecter les données aberrantes pour ne pas les confondre avec les valeurs extrêmes. Il est également important de montrer que les données sont indépendantes du temps.
2.2.1 Détection et Traitement des données aberrantes
Une donnée aberrante est une observation qui se trouve “loin” des autres observations (Moore et McCabe 1999). La présence d’une donnée aberrante peut signifier toutes sortes de choses. Cela peut être par exemple un cas qui ne fait pas partie de la population que l’on étudie (un adulte parmi un jeu de données concernant des enfants), ou bien une erreur de saisie ou de mesure.
Il existe de nombreuses méthodes de détection des données aberrantes, certaines basée sur la statistique, d’autres sur les mathématiques, d’autres encore sur l’analyse des données. Dans le cadre de notre travail nous utiliserons la méthode graphique, car elle est simple à mettre en œuvre.
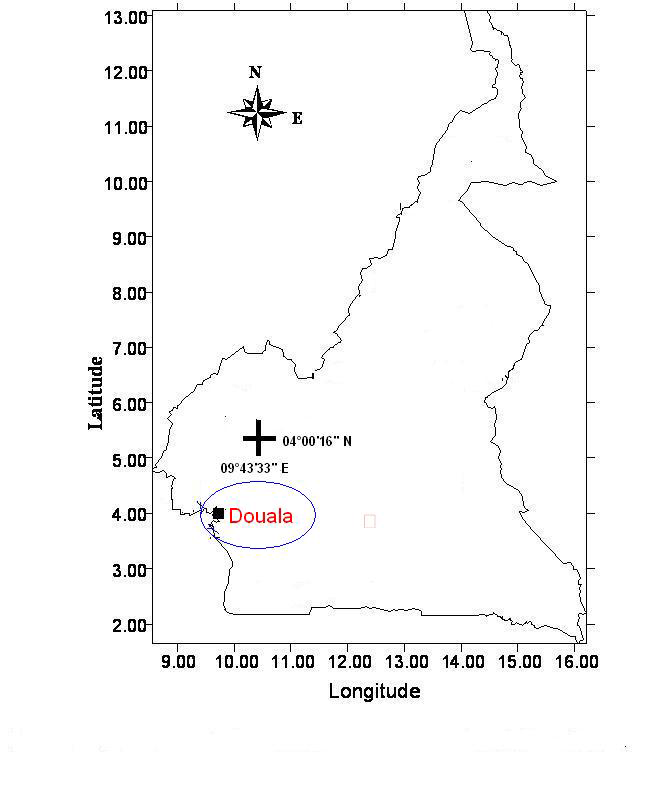
Figure 2.1 Zone d’étude et situation géographique de la station 64919 de Douala.(Anscombre, 1978)
2.1.1.1 Méthode graphique
La détection graphique est la méthode primaire de détection de données aberrantes. Elle peut d’ailleurs très bien fonctionner s’il existe une valeur extrême très à l’écart des autres. De plus, ce n’est pas une méthode “automatisée”, et elle ne s’applique a priori qu’à des données en 1, 2 ou 3 dimensions. la détection graphique peut être très utile, et présente l’avantage d’être très simple à déployer. Toutefois, elle ne peut s’appliquer qu’à des variables de petite taille, et sur de petites dimensions. De plus, elle reste une méthode très subjective, car visuelle. Nous avons le diagramme de dispersion des observations classées en fonction de leur rang, les boxplots ou boîte à moustaches et les graphiques des quantiles de valeurs brutes ou de résidus.
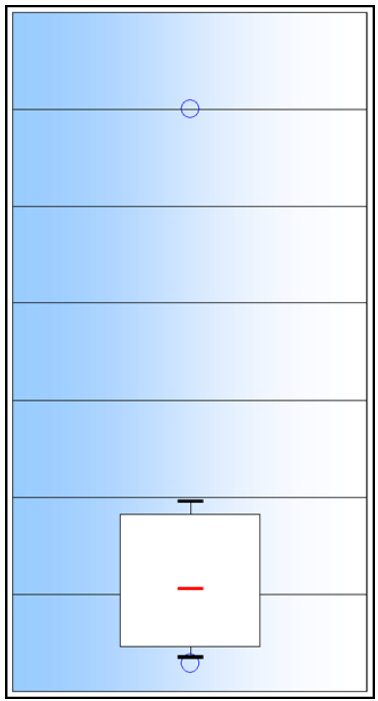
Figure 2.2 Boîte à moustache
(http.//zoonek2.free.fr/UNIX/48\_R\_2004/04.html,$2010$)
Le graphique de base en 1D est la boîte à moustaches (figure 2.2). Le trait central symbolise la médiane. Les bornes de la boîte blanche sont le premier et le troisième quartile. Les extrémités des moustaches sont le premier et neuvième décile. En n, les cercles sont le minimum et le maximum. Dans le cas présenté en exemple, ci-contre, le maximum est clairement éloigné du neuvième décile ! Ceci signifie que cette valeur est très éloignée du reste des données et peut ainsi être considérée vraisemblablement comme une donnée aberrante.
2.1.1.2 Traitement des données aberrantes
Il existe trois méthodes pour traiter les données aberrantes .
– Les valeurs aberrantes pouvant provenir d’erreurs de saisie, on vérifie si ce n’est pas le cas en retournant au questionnaire papier quand c’est possible et on corrige.
– On les rejette et on applique ensuite une des méthodes d’imputation (moyenne, médiane) vues pour les valeurs manquantes
– On adopte des méthodes qui diminuent leur impact au cours des analyses statistiques . la médiane et l’écart interquartile.
Il est important de noter que leur traitement relève d’une très grande complexité.
2.2.2 Étude de la corrélation entre les données et le temps
Étudier la corrélation entre les données et temps, c’est étudier l’intensité de la liaison qui peut exister entre ces deux variables. La liaison recherchée est une relation affine. Dans le cas de deux variables, il s’agit de la régression linéaire. Cette analyse permet d’étudier la tendance des données, c’est-à-dire s’ils ont tendance à augmenter (ou diminuer) avec le temps.
Une mesure de cette corrélation est obtenue par calcul du coefficient de corrélation linéaire. Par exemple, nous allons calculer le coefficient de corrélation entre deux variables X(x1, …….., xn) et Y (y1, …….., yn). On applique la formule suivante.
Si rp = 0, les deux variables ne sont pas corrélées. Les deux variables sont d’autant mieux corrélées que rp est proche de 1.
2.2.3 Description des modèles d’estimations des valeurs extrêmes
L’approche par la théorie des valeurs extrêmes (TVE) ne vise pas à modéliser ou à estimer la fonction de répartition inconnue F dans son ensemble, mais uniquement ses queues de distribution, qui sont seules utiles à la représentation des extrêmes (consulter l’annexe II, page 59). Les deux approches possibles sont . la première, dénommée block maxima method (BM) et la seconde approche est désignée sous le terme Peaks-Over-Threshold method (POT). En pratique, on se ramène dans les deux cas à un cadre de statistique paramétrique et d’ajustement de paramètres sur les données. Selon le contexte, l’une ou l’autre des approches peut se révéler mieux adaptée, mais il est le plus souvent utile de les mettre toutes deux en œuvre a n d’en comparer les résultats. L’échantillon statistique (données univariées) devant réunir des conditions d’indépendance et d’homogénéité, c’est-à-dire être identiquement distribué (i.i.d), notre analyse s’effectuera dans un cadre stationnaire. La plupart des analystes rejettent l’hypothèse du modèle Gaussien, comme méthode adéquate pour l’étude des événements extrêmes (Schär et al. 2004). Dans ce travail nous n’intéresserons qu’aux valeurs maximales de l’échantillon.
2.2.3.1 Le modèle des maxima par blocs . Block Maxima (BM).
La modélisation des queues de distribution par la méthode des maxima par blocs (Coles 2001, chapitre 3) s’appuie sur le théorème de Fisher-Tippet (Annexe II, page 59) et nous supposons que l’échantillon de maxima suit exactement une loi GEV, de la forme .
Il y a trois paramètres pour une fonction de GEV .
µ . un paramètre de position s’assimilant en quelque sorte à la moyenne pour une loi Normale.
σ. un paramètre d’échelle s’assimilant en quelque sorte à l’écart type (standard déviation) pour une loi normale centré réduite.
ɛ . un paramètre de forme, qui forme la distribution.
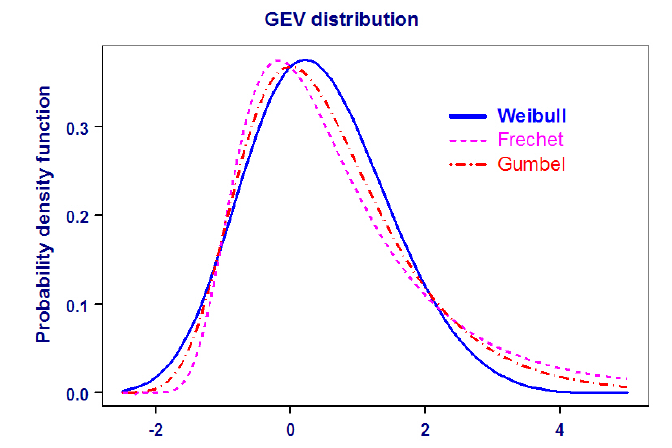
Les trois lois de probabilité vers les quelles la distribution de GEV converge, sont données par signe du paramètre ɛ. Nous obtenons la distribution de Weibull pour ɛ < 0, Gumbel pour ɛ -> 0 et Fréchet pour ɛ > 0 (figure 2.3).
Chacune de ces trois types de distributions ont un comportement distinct en termes de queue. La distribution de Weibull est à queue supérieur bornée, ce qui signifie qu’il existe une valeur nie donc le maximum ne peut dépasser. C’est celle des températures, des vitesses de vents et de niveau de mer. La distribution Gumbel avec une queue supérieur lumière et positivement asymétrique. Ceci signifie que, bien que les maximums peuvent prendre des valeurs infiniment élevée, la probabilité d’obtenir de tels niveaux devient exponentiellement petit, c’est celle utilisée couramment en hydrologie. La distribution de Fréchet avec une queue supérieur lourde et de moment in ni d’ordre supérieur, qui est une décroissance polynômiale de sorte que les valeurs supérieurs des maximums sont obtenue avec une plus grande probabilité comparé au cas de la queue lumière. Ce sont celles des précipitations, des impacts économiques et de ras de marées (voir figure 2.3).
Figure 2.3 Courbe de la fonction densité de probabilité de la distribution GEV
(generalized extreme value) avec µ= 0, σ = 1, ɛ = 0.2 (type Weibull ), ɛ = 0 (Gumbel ), et ɛ = 0.2. (http.//www.isse.ucar.edu/extremevalues/back.html(2009).)
L’estimation des paramètres du modèle est faite par les méthodes du maximum de vraisemblance (MV) et des moments pondérés (MP)
Cette méthode n’analyse que les valeurs maximales sur un intervalle de temps donné, souvent un an (maxima annuels), un mois (maxima mensuels) ou un jour (maxima journaliers). Elle consiste à un découpage des données en blocs, dont les maxima sont supposés distribués selon une loi d’une famille connue (GEV). Ce travail nécessite au préalable d’effectuée le choix de la taille des blocs, qui en réalité est importance pour la mise en œuvre de ce modèle.
a) Sélection de la taille des blocs
En considérant un échantillon de taille N, on choisit la taille k des blocs de telle sorte que la relation N = nk soit vérifiée. Ici n représente le nombre de blocs. La taille des blocs doit être suffisamment grand pour pouvoir s’appuyer sur un résultat asymptotique (Théorème de Fisher-Tippet . Annexe II page 59), c’est-à-dire limiter les biais. L’échantillon d’origine est ainsi réduit aux maxima de taille n, une distribution GEV (équation 2.7) est ensuite ajustée par le maximum de vraisemblance sur cet échantillon. La taille n de l’échantillon des maxima doit aussi être le plus grand possible pour limiter l’erreur d’échantillonnage dans l’estimation des paramètres µn, σn, et ɛn.
b) Estimation des paramètres du modèle BM
A partir de l’échantillon des maxima construit précédemment, nous pouvons estimer les paramètres de la GEV. Trois méthodes d’estimation sont envisageables . l’Estimation par le Maximum de Vraisemblance (EMV), par les Moments Pondérés (EMP) et par la méthode bayésienne (MB). Ici, nous ne verrons que l’EMV et l’EMP.
b-1) Estimation par le maximum de vraisemblance
Soit l’échantillon de maxima supposé iid, Y = (Y1, … , Yk) et hµ; σ; ɛ la densité de la loi GEV (x) (Equation 2.51). Cette dernière s’écrit pour ɛ# 0 .
Il fait appel à des procédures numériques (algorithme de Quasi-Newton) pour la maximisation de la vraisemblance. Alors le calcul des estimateurs ne pose pas de sérieux problèmes. En revanche, rien ne nous assure de leurs régularités (estimateurs asymptotiquement efficaces et normaux) surtout lorsque l’échantillon est de petite taille. Smith(1989), montre qu’il suffit que ɛ >= – 0.5 pour que les conditions de régularité de l’EMV soient remplies.
Précisons cependant qu’il n’existe pas de solution explicite à ces équations de maximisation (utilisation de méthodes numériques, type algorithmes de Newton-Raphson). L’avantage de cette technique, est le faite qu’elle offre une grande flexibilité.
b-2) Estimation par les moments pondérés
Il y a une alternative au maximum de vraisemblance . les moments pondérés. Nous avons les développement suivant . Pour r = 0, 1, 2,,,,, définissons βr par .
2.2.3.2 Le modèle de dépassement de seuil (POT) et la loi de Pareto généralisée (GPD)
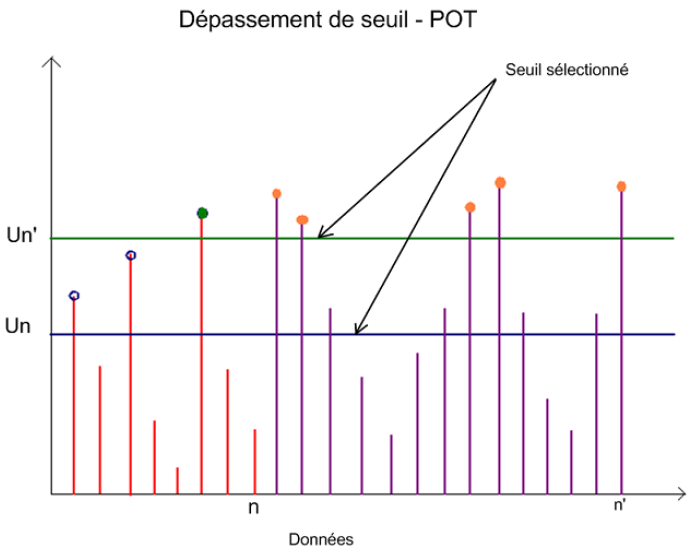
Fondée sur la théorie des valeurs extrêmes et encore connue sous le nom de Peaksover-threshold, elle est basée sur les travaux de J.Pickands (1975), A.C. Davison (2003) et R.L. Smith (1989). Cette méthode est récente et modélise des queues de distribution en s’appuyant sur le théorème de Balkema-de Haan-Pickands (Annexe II, page 60). Elle va impliquer le choix d’un seuil au-delà duquel le modèle peut être appliqué. Elle est sensible aux perturbations sur les données et aux hypothèses d’indépendance.
Cette deuxième méthode consiste à sélectionner un échantillon de pics indépendants en utilisant une méthode à seuil (figure 2.4). On suppose alors que les valeurs des pics au-dessus d’un seuil donnée u, sont réparties selon une distribution généralisée de Pareto (GPD), et que le processus d’occurrence des pics est poissonien. La loi GPD s’écrit pour un seuil u donné .
La valeur prise par le paramètre informe sur le poids des queues dans la distribution parente. En d’autres termes, plus les indices de queue sont élevés plus la distribution considérée possède des queues épaisses. Un indice de queue supérieur à zéro signifie donc que la probabilité d’occurrence d’événement extrême (dans le cas de la queue gauche) est plus importante que ce que prévoit la loi normale.
En comparant les équations (2.7) et (2.25), nous notons qu’ils ont le même paramètre de forme et ont la même interprétation pour les distributions de GPD et GEV. La seule différence est observée uniquement au niveau du paramètre d’échelle σ
Figure 2.4 Sélection d’échantillon de pics indépendants au-dessus de seuils données un et un’, par la méthode POT
La seule différence est observée uniquement au niveau du paramètre d’échelle e. Cette méthode modélise la distribution des valeurs dépassant un seuil donné. Elle consiste à sélectionner un échantillon de pics indépendants en utilisant une méthode à seuil. On suppose alors que les valeurs des pics sont réparties selon une distribution généralisée de Pareto (GPD), et que le processus d’occurrence des pics est poissonien (Equation 2.26).
a) Sélection de seuil
Théoriquement, il est possible de choisir le seuil u par optimisation du “trade-off” entre biais et efficience. En effet, pour une valeur u assez faible, les estimateurs seront biaisés et pour une valeur u assez élevée, le nombre d’observations extrêmes considérées dans l’étude se réduit, par conséquent on surestime la variance. En effet si le seuil est trop élevé, les écarts-types des estimateurs seront très importants. Il existe des techniques efficaces pour évaluer le seuil u, nous utilisons celles qui sont les plus utilisées à savoir . la fonction d’excès en moyenne (mean excess function ou mean residual life plot (ME-plot) en anglais) et la méthode dite du “stable scale and shape parameters”.
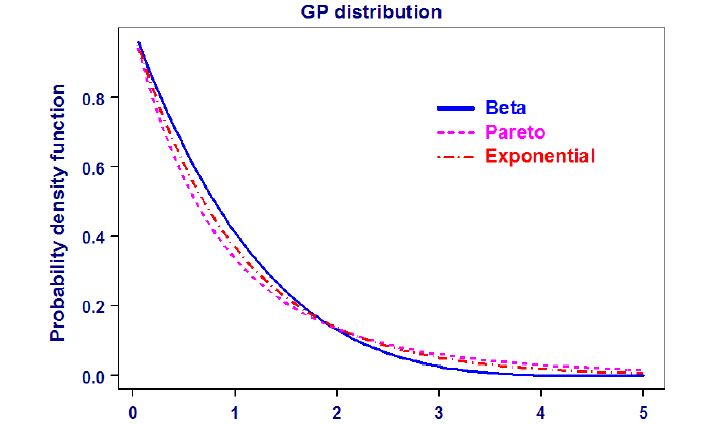
Figure 2.5 Courbe de la fonction de densité de probabilité de la distribution GPD
a-1) Fonction moyenne des excès (mean excess function ou mean residual life plot(ME-plot))
a-2) Méthode des graphes des paramètres d’échelle et de forme en fonction des différents seuils
Encore appelée “stable scale and shape parameters”, cette méthode essaie de déterminer un seuil requis, en ajustant les données à une distribution de GPD pour plusieurs rangs. chaque fois en utilisant un seuil différent. La stabilité des paramètres (forme et échelle) peut alors être contrôlé et localisée.
Cette technique est mise en œuvre par le biais des fonctions du paquet extremes (Gilleland et al., 2004) du logiciel système d’analyse statistique R. Ce paquet dispose d’outils objectifs pour déterminer la valeur du seuil, en examinant tout simplement la stabilité des paramètres de forme et d’échelle ɛ et σ.
b)Estimation des paramètres du modèle POT
Nous envisageons encore ici deux méthodes . l’Estimation par le Maximum de Vraisemblance (EMV) et celle par les Moments Pondérés (EMP).
b-1) Estimation par le maximum de vraisemblance
b-2) Estimation par les moments pondérés
Il peut arriver que certains moments n’existent pas, ne soient pas finis. Au lieu de la Méthode des Moments, nous utilisons alors la Méthode des Moments Pondérés. Définissons, avec r l’ordre du moment :
2.2.3.3 Périodes de retour et niveaux de retour
Typiquement, quand on considère les valeurs extrêmes d’un échantillon, on est intéressé par leurs niveaux de retour. On peut vouloir déterminer la probabilité d’occurrence d’une probable catastrophe (type tempête, canicule, inondation, etc.), à cette probabilité correspond une période de retour qui est une mesure de récurrence. Elle est données par .
Le niveau de retour d’un phénomène extrême est dé ni comme un quantile de ces distributions. Ce qui s’interprète, à l’aide de la loi géométrique (Annexe I page 58), comme l’intensité d’une variable (hauteur d’une crue, vitesse de vent, etc.), qui revient en moyenne tous les n années. Les notions de niveau de retour et la période de retour sont couramment utilisés pour transmettre des informations sur la probabilité d’événements rares tels que les inondations.
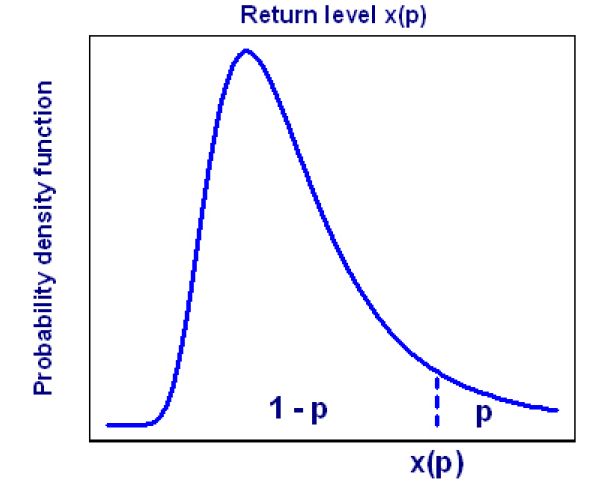
Un niveau de retour avec une période de retour années est un seuil élevé x(p) (par exemple, les flux de pointe annuelle d’un fleuve) dont la probabilité de dépassement est p. Par exemple, si p = 0.01, puis la période de retour est T = 100 ans. La période de retour est donc le niveau zT que l’on s’attend à dépasser, en moyenne, une fois toutes les T années. Le niveau de retour est déduite de la distribution parente (équation 2.7 ou 2.25), en établissant une égalité entre la distribution cumulative à la probabilité p ou quantile q désiré et ensuite déduire le niveau de retour zp. Déterminons zp pour chaque modèle.
Figure 2.6 Illustration du niveau de retour pour un seuil élévé x(p) et une probabilité de dépassement p.
(http.//www.isse.ucar.edu/extremevalues/back.html(2009))
a) Le modèle BM
La distribution de ce modèle étant donnée par l’équation 2.7, on dé ni le niveau de retour zp par .
On choisit p petit (valeur peu probable). L’estimation au maximum de vraisemblance de zp est obtenue en substituant dans la formule, les estimateurs au maximum de vraisemblance les trois paramètres du modèle (invariance du de vraisemblance).
b) Le modèle POT
Supposons que le modèle de dépassement au-dessus d’un seuil u soit de ce type, alors on a la relation .
2.2.3.4 Méthodes de calcul des intervalles de confiance
Des méthodes permettent l’estimation de l’intervalle de confiance pour les niveaux de retours, il s’agit des méthodes Delta et du Vraisemblance pro l, cette dernière est graphique.
a) Méthodes Delta
b) Méthodes du Pro l de vraisemblance
Cette méthode consiste à choisir un des paramètres (ici zp) et à considérer les autres comme des paramètres de nuisance. Considérons un ensemble de valeurs du paramètre d’intérêt (le niveau de retour). Pour chacune de ces valeurs, fixées, on calcule le maximum de vraisemblance (par rapport aux autres paramètres) et on trace la courbe obtenue. L’horizontale située en dessous du maximum de cette courbe à une distance de 0.5¬21 λ² (1 – α) quantile à (1 – α)% à un degré de liberté pour un paramètre à une dimension) coupe la courbe en deux points qui sont les extrémités de l’intervalle recherché. On peut obtenir des intervalles de confiance non symétriques, contrairement à la méthode Delta.
Les théorèmes de base précédents se placent dans le cadre i.i.d. (données indépendantes et identiquement distribuées). Cette hypothèse est souvent irréalisable pour des données météorologiques et climatiques. Des travaux récents se sont concentrés sur cette forme de dépendance et conduisent à introduire un paramètre supplémentaire θ (extrémal index compris entre 0 et 1) rendant compte du degré de regroupement dans le temps des extrêmes. Une propriété importante en pratique est que l’on peut d’abord ajuster une distribution GEV ou GPD comme si les données étaient i.i.d, puis estimer θ ensuite. Une fois le paramètre θ estime, les estimateurs des quantiles sont ajustes d’une façon qui rend compte de la propriété suivante . avec des données corrélées, le comportement des extrêmes dans un échantillon de taille N est comparable à celui des extrêmes d’un échantillon i.i.d. de taille réduite N θ .
2.2.3.5 Logiciels utilisés
Il existe quelques logiciels pour pouvoir travailler sur les valeurs extrêmes sans tout fois programmer soi-même. Pour traiter les données et appliquer les modèles nous avons utilisé la boîte à outils Extremes Toolkit . The Extremes Toolkit Weather and Climate Application of Extreme Value statistics, développée par NCAR et disponible sur le site . http.//www.assessment.ucar.edu/toolkit/. Cette boîte à outil contient des paquets (evd, extremes, ismev et evir) qui permettent à l’utilisateur d’estimer par le maximum de vraisemblance les paramètres des modèles BM et POT, de calculer les niveaux de retour et également d’obtenir le tracé des différents graphiques, ceci sous l’interface graphique du logiciel statistique R (R Development Core Team, 2004) disponible et téléchargeable sur le site . http.//cran.r-project.org/.
2.2.4 Conclusion
Les résultats précédents fournissent un cadre mathématique à l’analyse des extrêmes. Leur forme et leur rôle sont analogues à ceux du théorème de la limite centrale, lorsqu’il s’agit d’étudier les propriétés du maximum (ou minimum) sur un échantillon plutôt que celles de la valeur moyenne. Pour autant, leur utilité pratique n’est pas immédiate. Comme souligné précédemment, toutes les approches se heurtent au compromis à trouver entre biais et précision des estimations. Avec une procédure automatisée, ce choix peut cependant être guidé par l’ajustement de distributions GEV et GPD correspondant à différentes tailles de blocs et valeurs de seuil, puis la minimisation d’une distance entre distribution empirique et distribution estimée pour identifier le meilleur ajustement. L’application de ces modèles aux données de températures et précipitations maximales annuelles présente l’avantage d’une mise à jour annuelle, d’un bon ajustement en queue de distribution et l’existence d’intervalles de confiances. L’inconvénient provient du fait que pour des cumuls inférieurs à 24 heures nous avons une faible densité spéciale.
Retour au menu : Etude des Evénements Extrêmes : cas des Températures et Précipitations à Douala