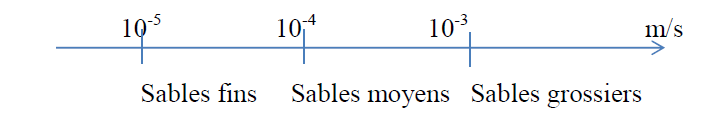De même qu’une granulométrie est faite au laboratoire, la porosité des sols est déterminée au laboratoire. Quant à la conductivité hydraulique, elle est faite in situ.
3.2.1. Mesure de la porosité efficace
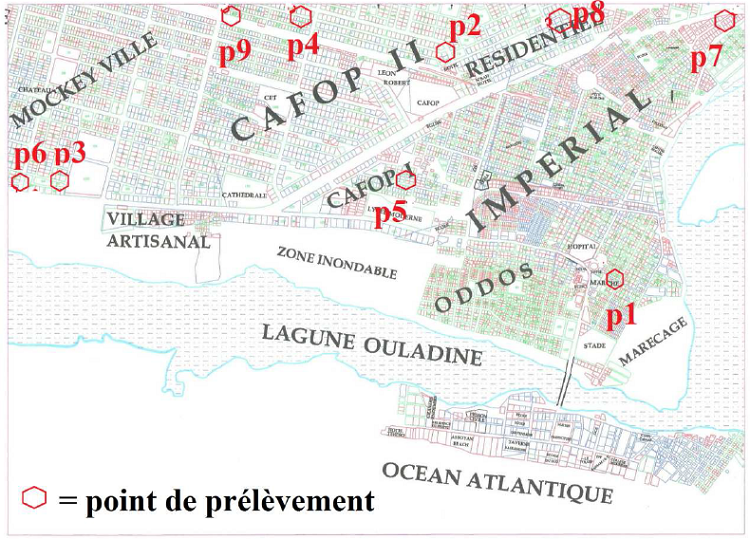
Sur le site, neuf échantillons de sol ont été prélevés à l’aide d’une tarière. Les points de prélèvement sont présentés dans la figure 6. Ces échantillons, conditionnés dans des sachets plastiques, ont été acheminés au laboratoire. Ils ont été pesés à l’aide de récipients jaugés puis saturés d’eau (Figure 7).
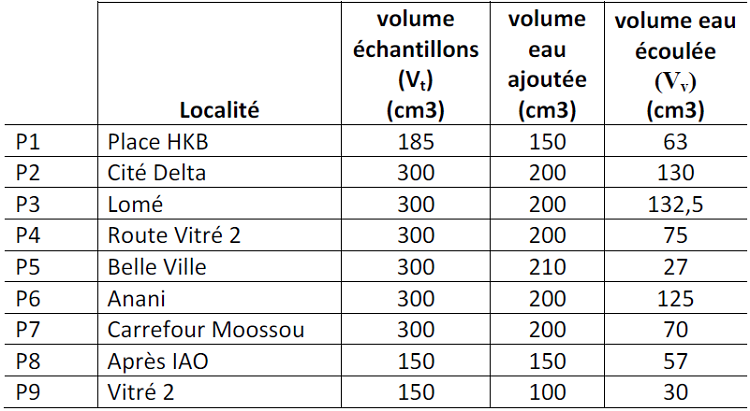
Après 48 heures d’égouttage, les volumes d’eau recueillis au niveau des échantillons ont été déterminés. Ces volumes ont permis de calculer les porosités efficaces à partir de la formule (1) :
n = Vv / Vt x 100 (1)
où Vv exprime le volume d’eau gravitaire en cm3 que le réservoir peut contenir à l’état saturé, puis libérer sous l’effet d’un égouttage complet ; Vt (cm3) est le volume de l’échantillon et n la porosité efficace. Le protocole de mesure est présenté dans la figure 7.
Figure 6 : Carte des sites de prélèvement des échantillons de sable
Figure 7 : Protocole de mesure au laboratoire de la porosité efficace
Les points de mesure et les différents volumes ayant permis de calculer les différentes porosités efficaces sont reportés dans le tableau I.
Tableau I : Récapitulatif sur les points de mesure de la porosité de drainage
3.2.2. Mesure de la conductivité hydraulique
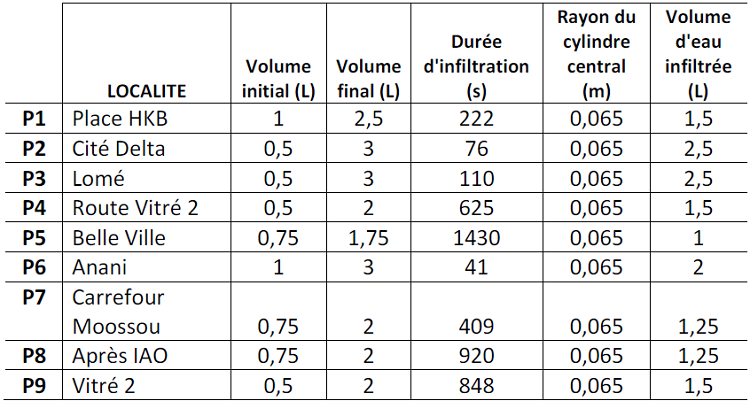
Pour mesurer la conductivité hydraulique, nous avons utilisé la méthode d’infiltrabilité à double anneau. La méthode d’infiltrabilité à double anneau est une méthode qui a été utilisée avec succès par Bovin et Touma (1988), et Koffi (2004) pour la mesure de la conductivité hydraulique des sols non saturés (Kouamé, 2007). La méthode à double anneau est basée sur la détermination de la vitesse verticale d’un flux d’eau à travers un sol à partir de la loi de Darcy. Pour cela, nous avons utilisé un infiltromètre dit de MUNTZ (Figure 8). Ce dispositif est constitué d’un cylindre métallique central d’environ 25 cm de hauteur et 13 cm de diamètre que l’on enfonce à 10 cm dans le sol et sur lequel on pose un vase de Mariotte qui maintient le niveau de l’eau constant à une certaine hauteur au-dessus de la surface du sol. Après la stabilisation de la vitesse, on mesure le volume d’eau infiltré pendant un temps T. Connaissant le débit q d’infiltration, q = V / T, on applique la loi de Darcy, l’infiltration se faisant suivant la surface S égale à la section du cylindre et le gradient hydraulique égal à 1. On a donc :
K = V / S.T (3)
Figure 8 : Dispositif de mesure de la conductivité hydraulique de la zone non saturée (Infiltromètre de MUNTZ)
Afin d’éviter que les filets liquides divergent au-dessous du cylindre central, on enfonce de 2 à 3 cm dans le sol un deuxième anneau plus grand, autour du premier, et on maintient un niveau d’eau constant dans l’espace annulaire.
Les mesures effectuées sur le terrain sont présentées dans le tableau II.
Tableau II : Récapitulatif sur les points de mesure de la conductivité hydraulique
Afin d’avoir une approche du type de sable de notre site à partir des valeurs de la conductivité hydraulique, nous avons utilisé la classification établie par Brassington (1988).
Classification établie par Brassington (1988).
3.2.3. Mesure de la granulométrie
3.2.3.1. Mode opératoire
150 g de nos échantillons de sol recueillis sont mis sur des papiers aluminium pour être séchés à l’étuve. Après 24 heures passées dans une étuve à 105oC, une quantité de 100 g des échantillons est prélevée. Celle-ci est introduite dans une colonne de tamis. Pendant 10 minutes, ces sédiments sont tamisés au moyen d’un agitateur à colonne vibrante. Après agitation, on pèse le refus de chaque tamis. On en déduit le pourcentage en poids de chaque classe dimensionnelle par rapport à l’échantillon de départ (Annexe 3).
Les méthodes de Friedman (1967) et Folk (1974) nous ont permis de déterminer la moyenne granulométrique (MZ) comme suit :
Mz = (d16+d50+d84)/3 (4)
Cette moyenne permet de définir les faciès granulométriques suivants :
• Sables très fins : 63 μm<Mz< 125 μm ;
• Sables fins : 125 μm<Mz< 250 μm ;
• Sables moyens : 250 μm<Mz< 500 μm ;
• Sables grossiers : Mz> 500 μm.
Où d16 est le diamètre des particules correspondant à un pourcentage pondéral de 16%, d50 est le diamètre des particules correspondant à un pourcentage pondéral de 50% d84 est le diamètre des particules correspondant à un pourcentage pondéral de 84%. d16, d50 et d84 sont exprimés en μm.
3.2.3.2. Construction des courbes granulométriques
Les courbes cumulatives semi-logarithmiques ont été utilisées pour représenter les paramètres granulométriques. La courbe cumulative semilogarithmique s’obtient en portant en ordonnée les refus cumulés de chaque tamis. Sur l’axe des abscisses ayant une graduation logarithmique sont portés les diamètres des tamis (Monde, 1997). Les dimensions intérieures des mailles des tamis correspondent aux diamètres des grains qui sont retenus à travers les mailles des tamis exprimé en mm. Elles sont portées en abscisses logarithmique en valeur décroissante à partir de l’origine. Le poids en pourcentage du poids total de l’échantillon étudié des fractions qui sont retenues à travers le tamis correspondant, sont portés en ordonné arithmétique. La courbe obtenue en joignant les points est la courbe granulométrique cumulative (Annexe 4).
3.2.4. Coefficient de corrélation
Le coefficient de corrélation R est un coefficient statistique permettant de mettre en évidence, une liaison entre deux types de séries de données statistiques.
Le coefficient de corrélation est compris entre 1 et -1 et on considère généralement que si sa valeur absolue est supérieure à 0,95, il y a une liaison forte entre les deux séries.
Si la valeur est proche de 1, les séries évoluent dans le même sens, si elle est proche de (– 1), elles évoluent en sens opposé.
La présence d’une corrélation n’est pas forcément la preuve d’une liaison de cause à effet, car les deux séries de données peuvent être influencées conjointement par une troisième.