Analyses bivariées
Raison de la venue et mémorisation du prix
Pour pouvoir croiser ces variables, nous allons effectuer un test Anova.
Nous posons dans un premier temps deux hypothèses :
H0 : les variances sont égales
H1 : les variances sont inégales
Nous avons un sig de 0,284 donc nous acceptons H0.
La seconde étape consiste à dire s’il existe une relation ou non, d’ou:
H0 : pas de relation
H1 : relation
Dans le cas présent, nous avons une signification de 0,494. H0 est accepté et donc nous pouvons dire qu’il n’existe pas de relation entre la raison de la venue en magasin et le fait de mémoriser les prix contenus dans les affiches de promotion en allée centrale
Choix de Auchan V2 et mémorisation du prix
Pour pouvoir croiser ces variables, nous allons effectuer un test Anova.
Nous posons dans un premier temps deux hypothèses :
H0 : les variances sont égales
H1 : les variances sont inégales
Nous avons un sig de 0,406 donc nous acceptons H0.
La seconde étape consiste à dire s’il existe une relation ou non, d’où :
H0 : pas de relation
H1 : relation
Dans cette situation, nous avons un sig de 0,609 et nous acceptons H0. Ainsi, il n’existe pas de relation entre le choix de Auchan V2 et la mémorisation du prix.
Raison de la venue en magasin et mémorisation des affiches
Récapitulatif du traitement des observations
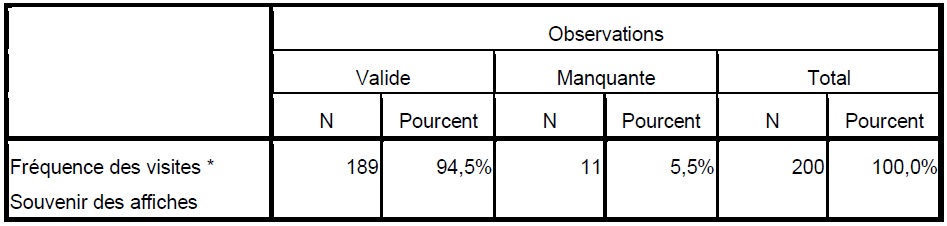
Nous procédons à un test du khi 2 pour traiter les données. Existe-t-il une relation entre la raison de la venue en magasin et la mémorisation des affiches au seuil de 5% ?
Nous posons ainsi deux hypothèses :
H0 : relation
H1 : pas de relation
Ici, le sig est de 0,72. Etant donnée qu’il est supérieur à 5 il n’y à pas de relation entre le fait de se souvenir d’une affiche promotionnel en fonction de la raison de la venue en magasin.
Fréquence des courses et mémorisation des affiches
Récapitulatif du traitement des observations
Nous procédons à un test du khi 2 pour traiter les données. Existe-t-il une relation entre la fréquence d’achat et la mémorisation des affiches au seuil de 5% ?
Nous posons ainsi deux hypothèses :
H0 : relation
H1 : pas de relation
Etant donné que nous avons un sig de 0,147, nous pouvons conclure H1, soit le fait qu’il n’y a pas de relation entre la fréquence des visites et la mémorisation des affiches.
Passage en allée centrale et Mémorisation
Nous procédons à un test du khi 2 pour traiter les données.
Néanmoins, il ne peut avoir interprétation des résultats car l’effectif est insuffisant pour faire l’analyse.
Temps de course et mémorisation
Afin de pouvoir savoir s’il existe une relation avec ces deux variables. Nous allons procéder à un Test T.
Existe-t-il une relation entre le temps de course et la mémorisation des affiches au seuil de 5% ?
Nous posons les hypothèses suivantes :
H0 : variances égales
H1 :variances inégales
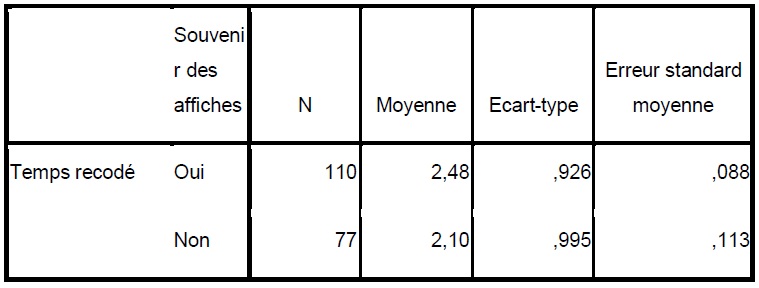
Statistiques de groupe
Avec un sig de 0,662 nous acceptons H1.
Le sig des variances inégales nous donne un résultat de 0,009 qui est donc supérieur à 5%.
Donc, nous pouvons dire qu’il existe une relation entre le temps de course et la mémorisation des affiches. Plus le temps de course est important, plus la mémorisation est facile.
Recherche des affiches de promotion et mémorisation des affiches
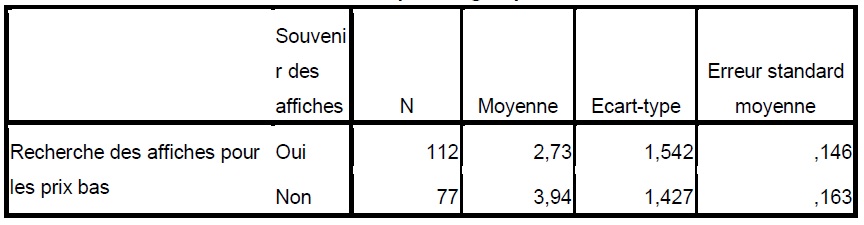
Statistiques de groupe
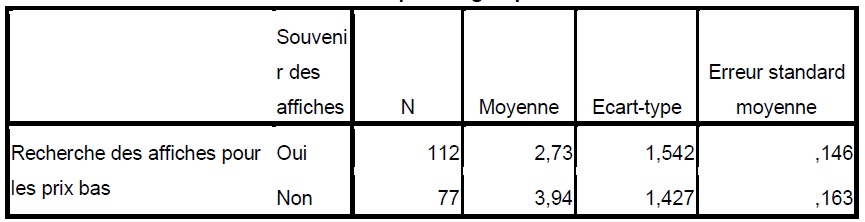
Afin de pouvoir savoir si il existe une relation avec ces deux variables, nous allons procéder à un Test T.
Existe-t-il une relation entre la recherche des affiches de promotion et la mémorisation de celle-ci au seuil de 5% ?
Nous posons les hypothèse suivantes :
H0 : variances égales
H1 :variances inégales
Avec un sig de 0,96 nous acceptons H1. Lorsque nous étudions les variances inégales, nous pouvons voir que le sig est de 0. Donc il existe une relation. Plus le client recherche les affiches, plus la mémorisation est facile.
