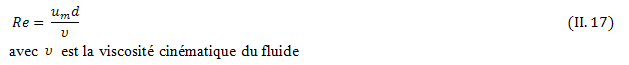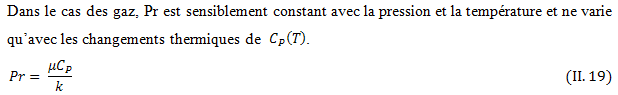II.1 INTRODUCTION
De tous temps, les problèmes de transmission d’énergie, et en particulier de la chaleur, ont eu une importance déterminante pour l’étude et le fonctionnement d’appareils tels que les générateurs de vapeur, les fours, les échangeurs, les évaporateurs, les condenseurs, etc., mais aussi pour des opérations de transformations chimiques. Les problèmes de transfert de chaleur sont nombreux, et on peut essayer de les différencier par les buts poursuivis dont les principaux sont [15] :
– l’augmentation de l’énergie transmise ou absorbée par une surface,
– l’obtention du meilleur rendement d’une source de chaleur,
– la réduction ou l’augmentation du passage d’un débit de chaleur d’un milieu à un autre.
Le transfert de chaleur au sein d’une phase ou, plus généralement, entre deux phases, se fait de trois façons :
– Par conduction,
– Par rayonnement,
– Par convection.
Un système de freinage a pour fonction principale de transformer une énergie mécanique en une énergie calorifique. Cette énergie se caractérise par un échauffement global du disque et des plaquettes lors d’une phase de freinage. Il est d’autant plus intéressant de simuler ce phénomène à plusieurs titres.
Pour cela et afin modéliser ce problème précisément, nous nous intéressons dans cette partie par le calcul du flux de la chaleur initial entrant dans le disque au niveau de la zone de contact.
II. 2 DEFINITIONS
II.2.1 Champ de température
Les transferts d’énergie sont déterminés à partir de l’évolution dans l’espace et dans le temps de la température : T= f(x, y, z, t). La valeur instantanée de la température en tout point de l’espace est un scalaire appelé champ de température. On distingue deux cas [16] :
– Champ de température indépendant du temps : le régime est dit permanent ou stationnaire.
– Evolution du champ de température avec le temps : le régime est dit variable ou instationnaire.
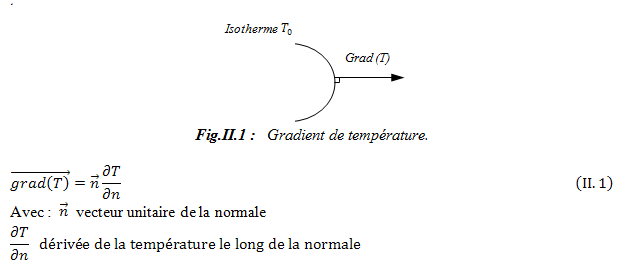
II.2.2 Gradient de température
Si l’on réunit tous les points de l’espace qui ont la même température, on obtient une surface dite isotherme. La variation de température par unité de longueur est maximale le long de la normale à la surface isotherme. Cette variation est caractérisée par le gradient de température [16]:
II.2.3 Flux de chaleur
La chaleur s’écoule sous l’influence d’un gradient de température par conduction des hautes vers les basses températures. La quantité de chaleur transmise par unité de temps et par unité d’aire de la surface isotherme est appelée densité de flux de chaleur, elle est exprimée en :
II.3 MODES DE TRANSFERT DE CHALEUR
Lorsque deux systèmes sont à des températures différentes, le système le plus chaud cède de la chaleur au plus froid. Il y a échange thermique ou encore transfert thermique entre ces deux systèmes. Cette situation se rencontre dans de nombreuses situations industrielles (moteurs thermiques ou même électriques, centrales électriques au fuel au gaz, etc…, électronique) ou domestique (chauffage de l’habitat)[17]. Un transfert d’énergie donne lieu à un flux de chaleur qui correspond à un déplacement de l’énergie du plus chaud vers le plus froid. Il existe trois modes essentiels de transferts de chaleur : la conduction, le rayonnement et la convection.
II.3.1 Conduction
C’est le transfert de chaleur au sein d’un milieu opaque, sans déplacement de matière, sous l’influence de différence de température. La propagation de la chaleur par conduction à l’intérieur d’un corps s’effectue selon deux mécanismes distincts : une transmission par les vibrations des atomes ou molécules et une transmission par les électrons libres.
Le transfert de chaleur par conduction s’appuie sur la loi de Fourier [16]:
Fig.II.2 : Lois de Fourier.
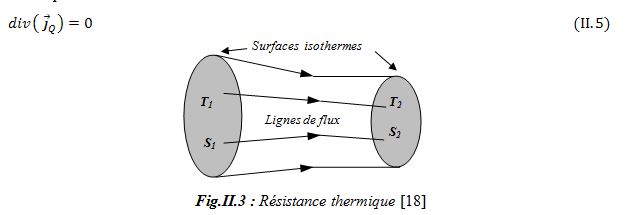
II.3.1.1 Résistance thermique
On considère deux surfaces isothermes S1 et S2 de températures T1 et T2 . Ces deux surfaces sont correspondantes c’est à dire que toute ligne de flux quittant la surface S1 atteint la surface S2. Pour un milieu conductif en régime permanent sans source interne, le bilan thermique s’écrit :
Appliquons, sur le volume fermé délimité par les deux surfaces isothermes S1 et S2 et la surface latérale constituée de toutes les lignes de flux s’appuyant sur le contour fermé délimitant les deux surfaces isothermes, le théorème d’Ostrogradsky [18],
II.3.1.2 Les régimes permanents
Ce sont les régimes pour lesquels la température en tout point du milieu est indépendante du temps, le déséquilibre est entretenu par les sources de chaleur [18].
II.3.1.3 Les régimes transitoires
Les régimes transitoires correspondent à l’évolution d’un système d’un état initial (permanent ou en équilibre) vers un état final (permanent ou en équilibre) provoquée par un changement à l’instant initial des sources; le champ de température T ( M ,t ) dépend du champ de température initial T ( M ,0 ) mais l’influence de celui-ci s’estompe avec le temps. A l’instant initial, au moins une source change, par contre elles demeurent constantes ensuite.
Les régimes transitoires ne doivent pas être confondus avec les régimes variables pour lesquels les sources évoluent au cours du temps [18]
La méthode générale de résolution par les fonctions de Green ne peut être envisagée sans posséder une bonne maîtrise préalable de la technique de séparation de variables avec développement en série de fonctions orthogonales.
II.3.2 Convection
La convection est un transfert de chaleur dans un milieu matériel avec mouvement de matière. Ce mode de transfert ne concerne donc que les fluides ou les échanges entre un solide et un fluide. Ce mécanisme de transfert est régi par la loi de Newton [16]:
La transmission de chaleur par convection est désignée, selon le mode d’écoulement du fluide, par convection libre et convection forcée. Lorsqu’il se produit au sein du fluide des courants dus simplement aux différences de température, on dit que la convection est naturelle ou libre. Par contre si le mouvement du fluide est provoqué par une action externe, telle une pompe ou un ventilateur, le processus est appelé convection forcée.
II.3.2.1 Le nombre de Reynolds
Ce nombre joue un rôle fondamental dans la caractérisation de l’écoulement ,il est définit par l’expression suivante [19] :
– Si Re < 2400 on est en régime laminaire.
– Pour des vitesses plus élevées, Re >> 2400, le régime turbulent apparaît
II.3.2.2 Le nombre de Nusselt
Ce nombre caractérise l’échange thermique entre le fluide et la paroi, il est définit comme suit [19] :
II.3.2.3 Le nombre de Prandtl
Ce nombre est entièrement caractéristique du fluide considéré [19]. L’inverse du nombre de Prandtl est appelé par les « thermiciens » français : le nombre de Stanton (S) .
II.3.3 Rayonnement
C’est un transfert d’énergie électromagnétique entre deux surfaces (même dans le vide). Dans les problèmes de conduction, on prend en compte le rayonnement entre un solide et le milieu environnant et dans ce cas, nous avons la relation [16]:
II.4 Stockage d’énergie
Le stockage d’énergie dans un corps correspond à une augmentation de son énergie interne au cours du temps d’où (à pression constante) [16] :
II.5 Les équations gouvernantes du transfert de chaleur transitoire par conduction
II.6 CALCUL DE FLUX DE CHALEUR ENTRANT DANS LE DISQUE
II.6.1 Introduction
Les performances en freinage des véhicules sont de toute évidence une des caractéristiques cruciales pour la sécurité. Dans la perspective d’accroître la sécurité, des efforts importants ont été consentis ces dernières années pour améliorer le freinage. Des normes réglementent le freinage dans la plupart des pays.
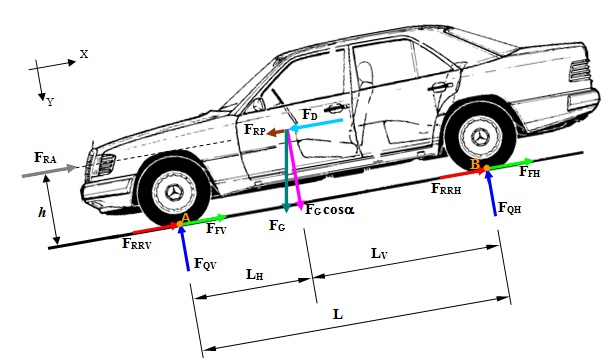
II.6.2 Les efforts agissant aux roues lors du freinage
Fig. II.6 : Définition des forces agissant sur une automobile lors du freinage
En observant la situation décrite à la Figure II.6, on peut écrire l’équilibre longitudinal et transversal du véhicule selon les axes x, y locaux de la voiture.
II.6.3 Puissance de freinage totale
II.6.4 Expression du flux thermique initial
Les disques de frein ont pour but de dissiper l’énergie mécanique en chaleur. Pour les trains ou les voitures, c’est l’énergie cinétique du véhicule qui est dissipée par le frottement des patins sur les disques. L’ensemble patin – disque s’échauffe sous cette action et refroidit à l’air ambiant. Ces freinages étant répétés, les disques de frein sont soumis à de la fatigue thermomécanique. Dans l’automobile, de nombreuses études ont montré que les freinages pouvaient engendrer des températures pouvant dépasser 700°C en quelques secondes.
Si on considère que le disque de frein peut absorber totalement la quantité de chaleur produite.
Page suivante : Chapitre III : Modélisation Thermomécanique du Problème