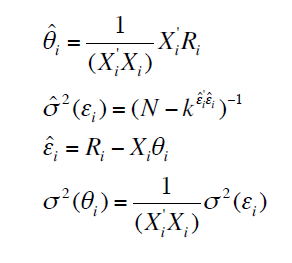I.I.2.1 MODÈLES THÉORIQUES
Dans ce mémoire de recherche, nous allons analyser deux méthodes couramment utilisées dans la littérature financière. Ces méthodes repèrent de façon efficiente la présence de trajectoire de cours anormaux. Selon Stephen J. Brown et Jerold B. Warner(11), il s’agit du :
– Modèle de moyenne (constant mean return model, « CMRM »)
– Modèle de marché (market modele, « MM »)
I.I.2.1.1 Modèle de moyenne
Attachée à l’évaluation du modèle de moyenne, l’évolution des taux de rentabilité de l’action i est formulée par :
I.I.2.1.2 Modèle de marché
Le modèle de marché fut initié par Sharpe(13) en 1963. Ce modèle postule pour une relation linéaire entre le taux de rentabilité Ri,t d’un actif et le taux
de rentabilité Rm,t de l’indice de référence, mesuré à partir de l’action i. Ce modèle s’inscrit donc dans le cadre d’une mesure de sensibilité du titre
étudié. Expressément, nous avons :
I.I.2.2 ÉVALUATION DES PARAMÈTRES
En ce qui concerne le modèle de moyenne, nous devons calculer un simple paramètre donné par la rentabilité moyenne μ de l’action i sur N, la période pour laquelle nous tirons nos taux de rentabilités normales. Le modèle de marché quant à lui requière l’intervention de deux paramètres distincts, à savoir αi et βi sur les mêmes périodes.
Pour ce faire, nous pouvons estimer l’ensemble des paramètres liés à chaque modèle à l’aide d’une représentation matricielle de la période N. A ce titre, nous pouvons consulter les études de John Y. Campbell, Andrew W. Lo et Craig MacKinlay, publiées en 1997(14). Deux composantes sont à calculer. Soit Ri, le vecteur composer des N taux de rentabilité et Xi :
– Un vecteur de N lignes égales à 1 pour le modèle de moyenne
– Une matrice à deux colonnes et N lignes dans le cas du modèle de marché dans laquelle les lignes de la première colonne sont égales à 1 et celles de la deuxième colonne prennent pour valeur le taux de rentabilité du marché en N.
– Enfin, nous avons un vecteur θi de paramètre agrégé au modèle utilisé, soit μi pour le modèle de moyenne, soit (αi,βi) pour le modèle de marché.
Cette représentation donne formellement l’équation suivante :
Pour chaque modèle, l’appréciation des paramètres peut aussi s’effectuer par le calcul des moindres carrés ordinaires (MCO). On peut observer à présent l’expression des différents estimateurs comme suit:
Où k désigne le nombre de paramètres du modèle utilisé.
– k = 1 pour le modèle de moyenne
– k = 2 pour le modèle de marché

13 Estimation de la valeur théorique d’un actif financier exprimé dans le « Capital Asset Pricing Model » (CAPM)
14 Ouvrage : « The econometrics of financial markets », Princeton University Press, Chapitre 4.