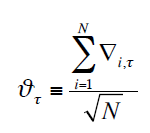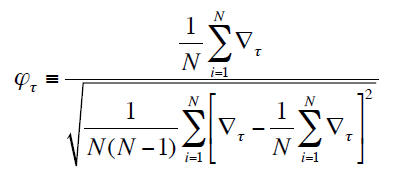Comment pouvons-nous juger de la significativité des tests réalisés selon les modèles théoriques réalisés précédemment ? Plusieurs étapes peuvent être mise en oeuvre pour en tirer une hypothèse viable. Afin de montrer la véracité du raisonnement utilisé dans cette étude, nous allons dans un premier temps étudier, en passant par la technique des moindres carrés ordinaires, un actif considéré indépendamment avant d’initier une analyse sur données associées.
I.I.4.1 MOINDRES CARRÉS ORDINAIRES
Dans la littérature économétrique, une rentabilité anormale est assimilable à un point aberrant par rapport à une suite de variables iid. Dans notre étude, nous usons des hypothèses classiques dans laquelle les moindres carrés ordinaires sont donnés par le vecteur des espérances des Ai lignes et de la matrice de variances-covariances des Ai lignes et des Ai colonnes de cette erreur. Nous avons :
I.I.4.2 RENTABILITÉS ANORMALES TRANSVERSALES ET CUMULÉS
L’analyse des rentabilités anormales transversale permet de juger de la signification d’un échantillon donné à une période t. Une quantité importante de travaux de recherche a été réalisée en fonction du comportement des rentabilités sélectionnées. Parce que nous travaillons sur les queues de distribution, ces statistiques vont avoir pour propriétés d’être asymptotiquement normales, d’espérance nulle et de variance égale à 1. La convergence vers la normalité étant vérifiée dès lors que le nombre de données est important (Brown et Warner) ou que le nombre d’actifs étudié soit supérieure ou égale à 30 (Pattel, Boehmer et al.). Les rentabilités anormales cumulées (RAC) permettent de juger de l’effet de la crise sur les différents actifs que peut détenir un actionnaire. C’est la représentation de l’amplitude des rentabilités anormales d’un échantillon sur une période donnée.
I.I.4.3 MÉTHODE DE BROWN ET WARNER
Nous avons donc les rentabilités anormales équipondérées de l’ensemble des titres sur la volatilité que peuvent générer celles-ci. C’est donc la rentabilité Ai obtenue divisée par le risque que celle-ci génère par ses variations erratiques en période de crise. Il est à noter que cette statistique implique une constance de la volatilité dans le temps. Nous pouvons aussi remarquer que cette hypothèse n’est plus vérifiée en phase de « partitionnement des données » ou « Clustering » dans lequel deux ou plusieurs titres réagissent, sur un intervalle de temps i, à un évènement lambda. Cette corrélation est exprimée à travers de nombreux exemples sur les marchés financiers.
I.I.4.4 MÉTHODE DE PATTEL
Le poids que peut donner un titre à forte volatilité historique dans le portefeuille est diminué. La statistique de Pattel prend la forme de :
I.I.4.5 MÉTHODE DE BOHEMER, MUSUMECI ET POULSEN
Faisant foi d’une robustesse plus importante lorsque la variance augmente, cette statistique cherche à valider ou non l’hypothèse selon laquelle A tend vers 0 pendant la période d’échantillonnage. La méthode de Bohemer, Musimeci et Poulsen s’exprime dès lors comme :
L’incertitude est au coeur de la logique financière. Le profil de risque que les investisseurs prennent à travers leurs positions est par conséquent déterminant. Le test des rentabilités anormales prend en compte deux paramètres : l’espérance mathématique et l’écart-type. Lorsque les marchés sont en équilibre, il est alors possible d’envisager une relation entre la rentabilité attendue et son risque intrinsèque, déterminé à partir de l’écart qu’il peut exister entre la rentabilité moyenne historique amenée par cette dernière. Le test des fréquences anormales sur un temps long a donc pour objet de connaître l’ampleur, mais aussi la durée, que peut amener de telles rentabilités en période d’incertitude. Nous pouvons désormais reconnaître, de façon plus rigoureuse, l’état de crise, la quantifier, peut-être la comparer.
Cette introduction nous amène à penser qu’il est nécessaire d’établir une solide gestion de mesure des risques.
15 Nous devons savoir si l’analyse de cette dernière donnée est homoscédastique. En cas contraire, le risque spécifique peut biaiser les calculs. Boehmer se propose d’étudier se corollaire à travers une étude statistique.