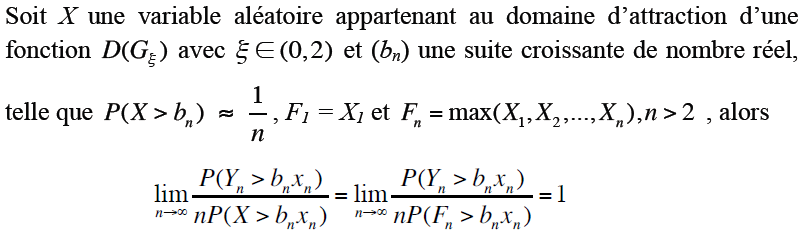« Les théoriciens classiques ressemblent à des géomètres euclidiens qui, dans un monde non-euclidien découvrant par l’expérience que des lignes droites parallèles se rencontrent souvent, reprocheraient aux lignes de ne pas rester droites – comme seule remède aux collisions malheureuses qui se produisent. Pourtant, en vérité, il n’existe pas d’autre remède que de se débarrasser de l’axiome des parallèles et de travailler dans une géométrie non-euclidienne. C’est une chose similaire qui est requise aujourd’hui en économie »
John Maynard Keynes
La théorie des valeurs extrêmes (TVE) est étudiée dans le cadre de la recherche d’évènements rares d’une suite de variables aléatoires indépendantes et identiquement identifiées. L’observation des cours des actifs financiers montre que ceux-ci sont hypothétiquement influencés par leurs cours passés, auquel l’aléa est souvent modélisé par un mouvement brownien géométrique. La théorie des valeurs extrêmes est donc un cas particulier de ce mouvement. L’intérêt concret de l’étude des extrêmes se trouve dans l’analyse des maxima et des minima des séries statistiques concernées.
Sur les marchés financiers, nous gardons toujours à l’esprit les grandes crises qui ont marquées notre histoire, poussant les actifs à atteindre des valeurs extrêmes comme pour la crise des Subprimes. En outre, bien connaître la distribution maximum et minimum se révèle être un excellent outil d’aide à la décision, voire une opportunité de gestion en temps de crise.
La Théorie des Valeurs Extrêmes s’intéresse non pas à la modélisation totale d’une distribution mais seulement aux queues des lois spécifiques(25).
Deux théorèmes sont indispensables pour une bonne compréhension de la Théorie des Valeurs Extrêmes : celui de Fisher- Tippet et celui de Balkemade Haan-Picklands. Deux méthodes principales de modélisation des évènements rares sont possibles : La méthode « Block Maxima » (BM) qui modélise la distribution des extrêmes par la Generalized Extreme Value Theory (GEV) dérivant explicitement du théorème de Fisher-Tipett, et la méthode « Peaks Over Theshold » (POT) qui modélise la distribution des excés au-dessus d’un seuil élevé (faisant apparaître les queues de distribution) par la Generalized Pareto Distribution (GPD) estimé par le théorème de Balkema-de Haan-Picklands. Cette dernière méthode sera modélisée en fréquence des rentabilités anormales afin d’estimer le paramètre u de la crise des Subprimes.
I.II.2 1 ÉTUDES FONDAMENTALES
Concernant la loi faible des grands nombres, rappelons cependant les études fondamentales permettant de lier la théorie fondée sur le comportement asymptotique de la distribution d’une somme de variable aléatoire et celui de la distribution du maximum et du minimum.
Cela nous permet de connaître la probabilité, pour un nombre n grand, du dépassement d’un seuil x par l’ensemble de la composition d’une suite de n variables aléatoires. Lorsqu’une de ces variables se présente de façon extrême par rapport aux valeurs prises par chacun des autres éléments de la suite, nous considérons que le seuil x a été franchi. Ceci caractérise l’événement rare dont nous cherchons à étudier la distribution.
I.II.2.2 LOIS DES MAXIMA : RÉSULTAT EXACTS
Le phénomène empirique suit une marche aléatoire, mesuré par une variable X, décrivant l’évolution du prix d’un actif financier. La variable aléatoire X présente la rentabilité logarithmique. Nous dénommons
– gX la fonction de densité notée [l,u]
– GX la fonction de répartition de probabilité de la variable aléatoire X.
25 Voir Embrechts, Kluppelberg, Mikosch et Beirlant, Goegebeur, Segers, Teugels pour plus d’approfondissements.
26 Dans une masse de Dirac, mesuré a partir d’un espace ———————————–