II.II.2.1 RÉALITÉ ERRATIQUE
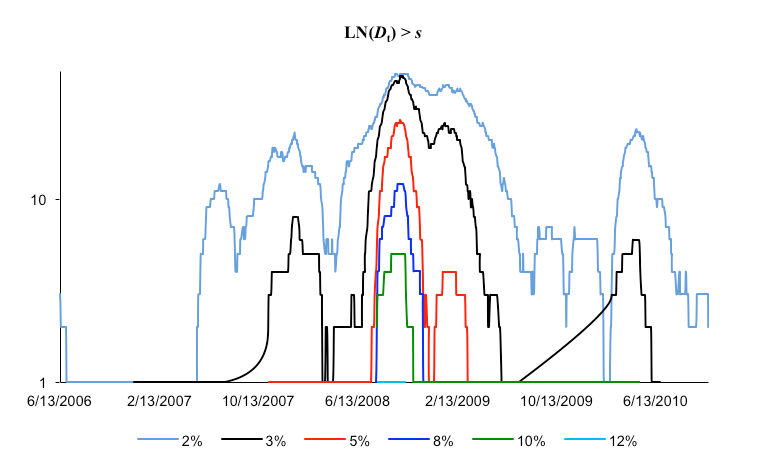
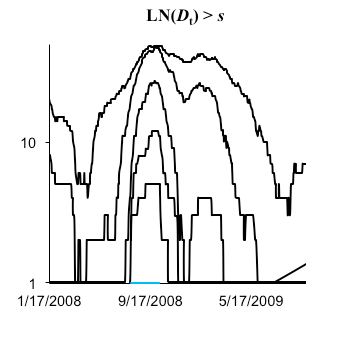
Nous donnons ci-après deux représentations graphiques qui permettent de visualiser les valeurs ayant dépassées s. Nous avons préféré les présenter à partir d’une échelle logarithmique, plutôt que sur échelle linéaire simple. Lorsque l’on exprime un nombre en logarithme, on effectue une mise à l’échelle ce qui permet, plutôt que de se concentrer sur la valeur absolue du nombre comme on le fait couramment, de le comparer aux autres nombres qui l’entourent. Ainsi, nous pourrons juger de la pertinence de chaque seuil sur la fenêtre F = 50.
Les résultats sont évocateurs. Les variations laissent apparaître une majorité des variations journalières supérieures ou égales à 3%. Celles-ci se concentrent sur une période de 615 jours, du 17/01/2008 au 23/09/2009.
Cela représente 53.57% des données de l’étude(46). Le DJIA, pendant la crise des Subprimes, a donc connu statistiquement une distribution des cours formant des queues de distribution épaisses en valeur absolue.
Nous pouvons aussi émettre l’idée qu’il y a eu un effet « Clustering » et un effet « Momentum(47) » sur la période ventrale.
II.II.2.2 SÉLECTION DE SEUIL
Deux méthodes statistiques de modélisation des queues sont possibles :
– La méthode BM
– La méthode POT
En finance de marché, nous allons privilégier la méthode POT, plus adaptée, notamment parce qu’elle va en adéquation avec un phénomène couramment observé : Le « clustering(48) ». De plus, comparée à la méthode BM, qui ne considère pas toutes les valeurs susceptibles d’être extrêmes (49) , cette méthode est à la fois plus flexible et plus réaliste.
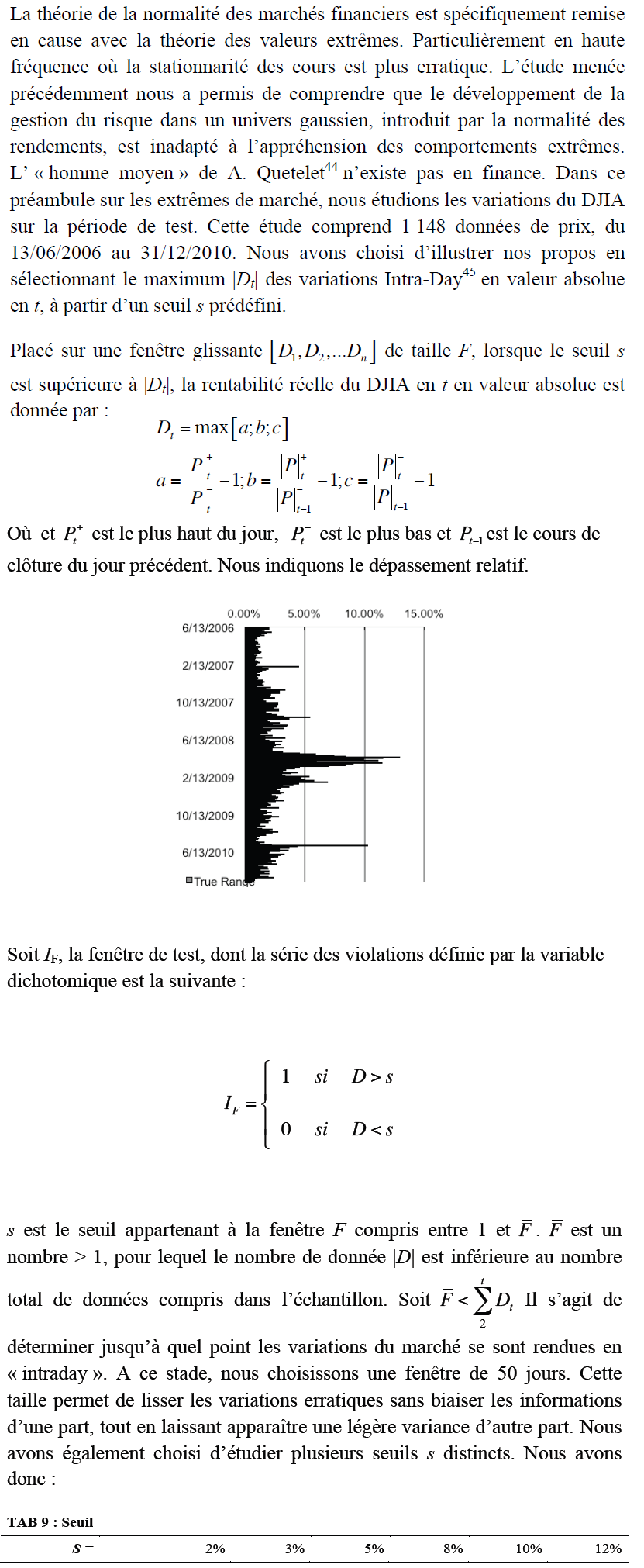
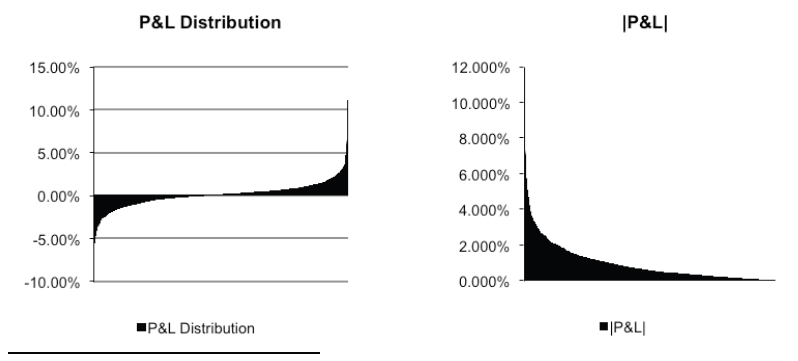
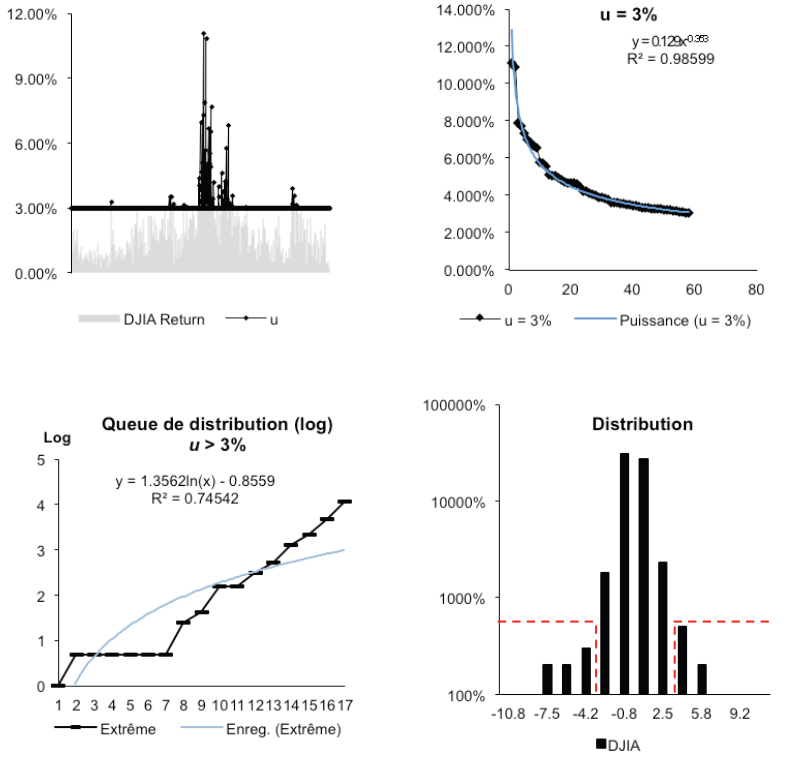
Cette modélisation de queue de distribution engage un échantillon au-dessus du seuil u, lequel conduit à une forme de loi GPD. Les méthodes utilisées reposent sur le comportement graphique des valeurs considérées supérieures à un seuil. Ces deux graphiques montrent d’une part la variation décroissante du DJIA pendant la crise des subprimes. D’autre part, la variation décroissante en valeur absolue. Remarquons le caractère asymptotique de la courbe. Le nombre de valeurs se réduisant lorsque l’on approche la valeur nulle de l’abscisse. Il est alors délicat de choisir un seuil u grand pour que l’estimation de la distribution de Pareto généralisée soit valide. Celui-ci ne peut également pas être trop élevé pour garder une certaine cohérence avec le comportement réelle du cours du DJIA. Le nombre de données supérieur à u défini est en rapport direct avec l’espérance future d’observer un tel évènement. Nous constatons au vu du tableau présenté ci-dessous qu’il existe très peu de variation supérieure à 5% (soit 4,86% des échanges). Environ la même quantité est observée pour les valeurs dépassant 4%. Les valeurs inférieures à 3% semblent cohérentes en terme de volume d’observations, cependant, celles-ci risquent de biaiser le modèle, se rapprochant trop de la tendance centrale.
Nous présentons donc un seuil u = 0.03. Nous obtenons 58 données. Le graphique ci-contre représente ce seuil, qui semble correspondre aux valeurs extrêmes présentées par la théorie.
44 A. Quetelet est un mathématicien, astronome, naturaliste et statisticien belge du XIXème siècle. Il présenta dans son ouvrage : « Sur l’homme et le développement de ses facultés, essai d’une physique social » la notion d’homme moyen. « L’homme moyen d’une population est un individu dont les caractéristiques physiologiques sont chacune égale à la moyenne des autres caractéristiques physiologiques de la population »
45 Ensemble des variations comprises dans une journée boursière.
46 Le calcul est le suivant : (615/1148).100 = 53, 57
47 La Théorie des Marchés Efficients (Efficient Market Theory) soutient que les marchés fonctionnent de manière à retranscrire intégralement et instantanément l’ensemble des informations disponibles. Jegadeesh et Titman, en 1993, mettent en évidence l’effet « momentum ». Ils observent que la tendance des titres par rapport au marché semble se poursuivre dans une mouvance irrationnelle. Il en va de même pour la variance journalière dans ce contexte.
48 Le phénomène de cluster, vu précédemment en section théorique, se défini comme une grappe de volatilités caractéristiques des rentabilités liées aux actifs financiers.
49 La méthode BM extrait le maximum de chaque période définie préalablement. Elle ne prend donc pas en compte certaines données extrêmes liées aux cycles financiers et peut en revanche prendre des valeurs faibles lors des blocks précédents.