La variation des prix ou les rentabilités importe plus que ces mêmes prix dans la détermination du taux de couverture. Les rentabilités du spot comme du « future » sont caractérisées, comme la plupart des variables financières, par des « fat tails » ou « queues épaisses » et asymétrie qui s’écartent de la loi standard et classique dite « loi normale ». « Se couvrir » contre le risque requiert en même temps le mesurer avec des outils. Mesurer le risque c’est simultanément jauger l’occurrence faible des valeurs extrêmes par rapport aux valeurs moyennes.
La détermination du taux de couverture avec comme mesure de risque l’écart-type et ou la value at risk est compromise par la non-normalité et l’épaisseur de queue, mais aussi les « upsiderisk » ou les risques de hausses bénéfiques pour le producteur qui sont pas pris en compte par l’écart-type, ce qui en gros sous-estime le risque. Pour corriger ces anomalies d’autres mesures sont applicables afin de déterminer le nombre optimal de contrat à souscrire, comme la value At risk Cornish –Ficher prenant en compte l’asymétrie et l’excès de Kurtosis, la distribution de student caractérisée par une queue plus épaisse, ainsi que la semi-variance qui traite unilatéralement les « mauvais risques ». Des mesures de dominance stochastique comme la moyenne LPM l’acronyme de « low partial moment » sont minimisés afin de trouver le taux de couverture optimal. Une minimisation du coefficient d’aplatissement a-t-il été nécessaire, ainsi que l’usage de la théorie des valeurs extrêmes.
L’usage de la distribution de Johnson, qui transforme une variable aléatoire en variable standard normal, est envisagé pour améliorer la normalité des rendements. Dans un second lieu, les taux de couverture sont revus en cas de dépassement de la perte potentielle suggérée par les mesures de risque utilisées. Les rentabilités des positions résultantes issues des diverses mesures de risque sont soumis à un ré-échantillonnage, par « bootstrapping » , et enfin à la mesure d’inégalité bien connue qu’est l’indice de Gini. L’indicateur de Gini mesure, en le multipliant par la moyenne de la distribution, l’écart moyen qui existe entre deux valeurs, prises au hasard dans la distribution. Son utilisation permet d’évaluer les inégalités d’une population à l’intérieur des groupes et entre les groupes. La mesure d’inégalité de Gini (G), comprise dans l’intervalle fermé [0,1], est habituellement appliquée à des distributions de revenu.
Lorsque G est élevé, la répartition des revenus est jugée inégalitaire alors que les faibles valeurs renvoient à des répartitions égalitaires. La décomposition est une méthode non paramétrique qui s’applique lorsqu’une population regroupe plusieurs sous-populations (groupes).
Dans ce cas, il est possible de scinder l’indicateur en deux composantes : les inégalités observées à l’intérieur des groupes (mesures intragroupes) et les inégalités observées entre les groupes (mesures intergroupes). Par cette méthode, il est possible de rapprocher le risque aux inégalités. Pour établir ce lien, il faut admettre que lorsque l’indicateur tend vers 1 (distribution inégalitaire), la distribution renvoie à un actif risqué et quand il tend vers 0 (distribution égalitaire), le titre est non risqué, puisque alors le rendement est le même sur n périodes successives. Dans ce cadre, nous admettons implicitement que les résultats vont porter sur des inégalités de rendement au cours du temps. Le recours à l’indicateur de Gini tient compte des moments d’ordre.
Selon l’approche shalit et yitzhaki, soient deux variables aléatoires continues Z_1 et Z_2 d’une même fonction de distribution f(z) et F(z) étant respectivement les fonctions de densité et de répartition.
Avec Z compris entre a et b (a
∫_a^b▒〖f(z)dz=〗 ∫_(z=a)^b▒〖dF(z)=1〗
Et F(z)=∫_a^z▒f(z)dz
Ce qui implique F(a)=0 etF(b)=1.
Le coefficient de Fini correspond à un demi de l’espérance de la valeur absolue de la différence entre Z_1 et Z_2 :
Γ=1/2 E(|Z_1-Z_2 |
Selon Dorfman , la valeur absolue de cette différence peut être réécrite de la façon suivante :
|Z_1-Z_2 |=Z_1+Z_2-2min(Z_1 〖,Z〗_2)
Ce qui donne :
Γ=1/2(E(Z_1)+E(Z_2)-2E(mi n(Z_1 〖,Z〗_2 ))
La moyenne µ est identique à E(Z_1 )=E(Z_2 )=∫_a^b▒〖zf(z)dz=〗 ∫_(z=a)^b▒zdF(z)
Soit z une valeur quelconque de la fonction de densité f(z). Les probabilités que Z_1 et Z_2 soient supérieures à z, et Z_1 ou Z_2 ne soit supérieure à z doivent être égale à 1.
Avec Prob(Z_1≤z)=Prob(Z_2≤z)=F(z)
La probabilité qu’à la fois Z_1 et Z_2 soient supérieures à z est donnée par :
Prob(Z_1>z)*Prob(Z_2>z)=[1-F(z)]²
La probabilité qu’au moins Z_1 ou Z_2 ne soit pas supérieure à z est équivalente à la probabilité que le minimum entre Z_1 et Z_2 ne soit supérieur à Z. on a :
Prob[mi n(Z_1 〖,Z〗_2 )≤z]=1-Prob(Z_1>z)*Prob(Z_2>z)=1-[1-F(z)]²
La probabilité Prob[mi n(Z_1 〖,Z〗_2 )≤z] peut être prise comme la valeur de la fonction de répartition g(y) de la variable aléatoire y=min(Z_1 〖,Z〗_2) au point y=z entre a et b.
E(mi n(Z_1 〖,Z〗_2 ) )=∫_(z=a)^b▒ydG(y)
Ceci est équivaut à :
∫_(z=a)^b▒〖zdG(z)=zd〗 {1-[1-F(z)]^2 }=2∫_(z=a)^b▒〖z[1-F(z)]dF(z)〗
Le coefficient de gini devient :
Γ=µ-2∫_(z=a)^b▒〖z[1-F(z)]dF(z)〗=2∫_(z=a)^b▒〖z[F(z)-1/2]dF(z)〗
Etant donné que :
E(F(z))=∫_(z=a)^b▒F(z) dF(z)=1/2 {F(b)^2-F(a)^2 }=1/2
∫_(z=a)^b▒〖{F(z)-E(F(z)}〗 dF(z)=0
Et
∫_(z=a)^b▒〖E(z){F(z)-E(F(z)}〗 dF(z)=E(z)∫_(z=a)^b▒〖{F(z)-E(F(z)}〗 dF(z)=0
Le coefficient de gini est alors : Γ=2∫_(z=a)^b▒〖[z-E(z)]{F(z)-E(z)}〗 dF(z)
La covariance de deux variables aléatoires étant l’espérance du produit de leur écart par rapport à leurs moyennes, on peut écrire dans ce cas que l’indice de gini vaut :
Γ=2cov(z,F(z))
Nous avons montré que le coefficient de gini d’une variable aléatoire correspond à deux fois la covariance entre cette même variable et sa fonction de répartition.
En statistiques, les techniques de bootstrap sont des méthodes d’Inférence statistique modernes, datant de la fin des années 70. L’objectif est de connaître certaines indications sur une statistique : son estimation bien sûr, mais aussi la dispersion (variance, écart-type), des intervalles de confiance voire un Test d’hypothèse. Cette méthode est basée sur des simulations, comme les méthodes de Monte-Carlo, les méthodes numériques bayésiennes, l’algorithme de Metropolis-Hastings , à la différence près que le bootstrap ne nécessite pas d’information supplémentaire que celle disponible dans l’échantillon.
En général, il est basé sur de « nouveaux échantillons » obtenus par tirage avec remise à partir de l’échantillon initial.(la procédure est détaillée en annexe).
Dans notre cas, le ré –échantillonnage est utilisé pour un calcul non-paramétrique de la value at risk en reconstituant la distribution des rendements de la position résultante sous l’hypothèse forte de rendements indépendamment et identiquement distribués.
Les rendements mensuels sont caractérisés de la façon suivante :
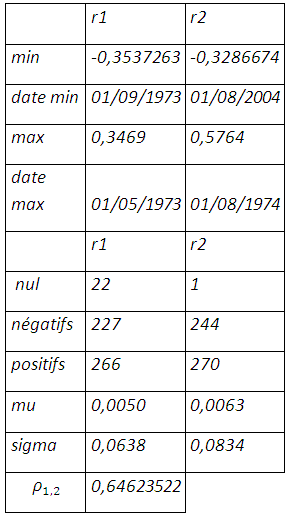
De janvier 1969 à décembre 2011, il y a eu 22 fois où le prix au comptant du soja n’a pas évolué contre 227 rendements négatifs dont le pire est enregistré en septembre 1973, année de la crise pétrolière pendant laquelle simultanément en septembre on enregistre le rendement le plus élevé au mois de Mai. Le future enregistre plus de rendements positifs et négatifs mais un seul rendement nul dont les positifs l’emportent sur les négatifs avec une plus grande différence pour le prix au comptant. Les rendements du soja sont en moyenne inférieurs à celui du future et enregistrent moins de déviations par rapport à leur moyenne.
1-L’écart-type comme mesure de risque
Bien entendu en se référant à la théorie de portefeuille efficient de Markowitz , le risque est mesuré par l’écart-type qui est la racine de la somme des écarts à la moyenne. On suppose que les prix cash et futures du soja suivent une loi normale. La position résultante s’établit comme suit :
R_P=r_(1 )-〖hr〗_2
R_P étant rendement mensuel de la position résultant de la couverture, r_1 le rendement mensuel du prix cash et 〖 r〗_2 le rendement mensuel du prix future.
La variance de la position résultante est donnée par : σ_P^2 = σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2
σ_P^(2:) la variance du rendement de la position couverte
σ_1^2: la variance du rendement spot mensuel
σ_2^2 : la variance du rendement future mensuel et ρ_1,2 le coefficient de corrélation entre le rendement du spot et celui du future.
La valeur de h qui minimise la variance est donnée par le programme d’optimisation suivant en minimisant le risque :
〖MIN〗_h σ_P^2 = σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 s/c h≤1
La valeur du taux de couverture est le rapport entre la covariance entre le prix anticipé et le prix spot à la variance du prix anticipé sur le marché à terme : h=ρ_1,2 σ_1/σ_2
L’implémentation sous Excel donne le résultat suivant :
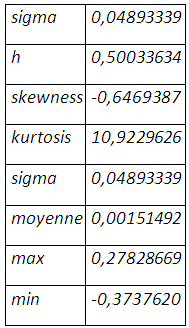
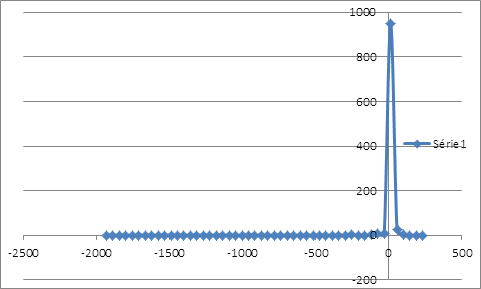
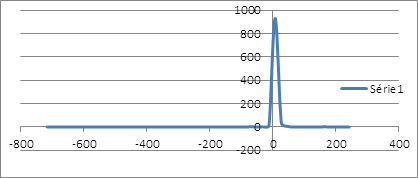
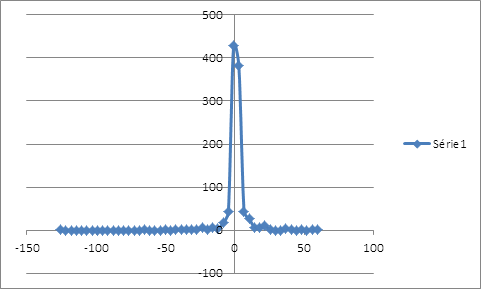
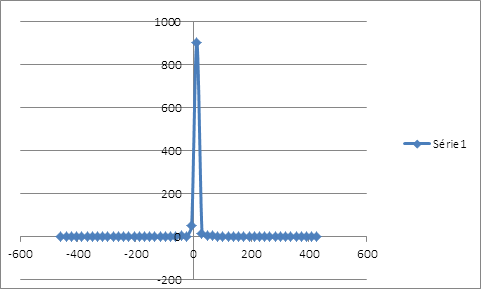
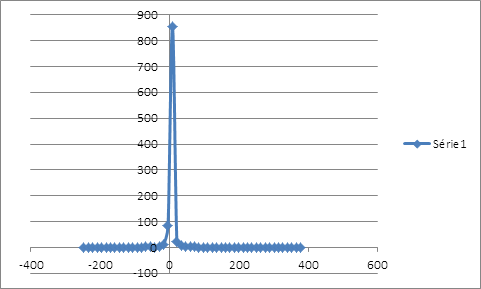
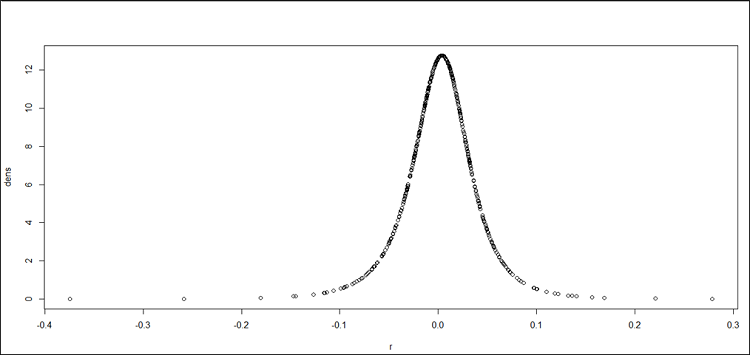
La minimisation de l’écart-type, comme mesure de risque, suggère un taux de couverture 50,033% qui laisse une distribution asymétrique étalée vers la gauche sans compter l’épaisseur de queue.
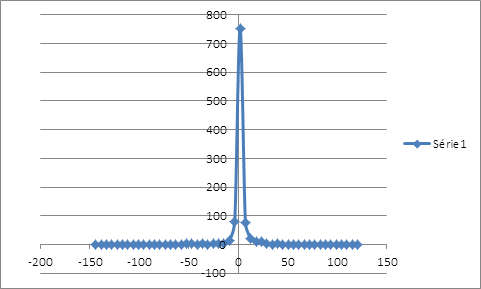
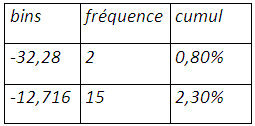
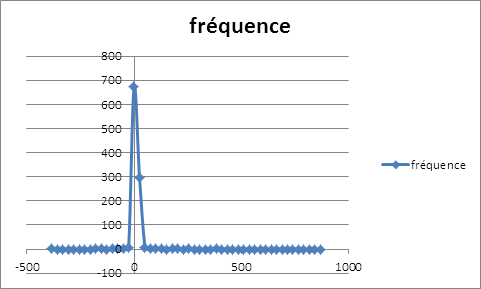
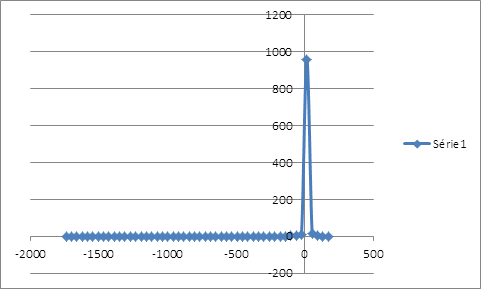
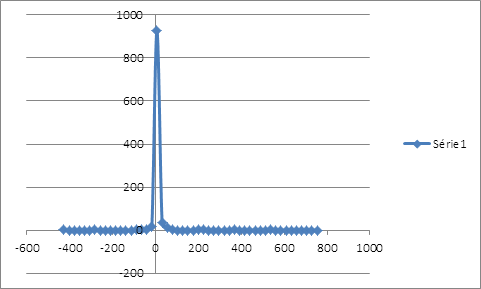
La distribution des rendements de la position couverte issue du ré-échantillonnage possède un seul mode au niveau des rendements nuls et étalée plus à gauche qu’à droite. La distribution des rentabilités est loin de suivre la loi de gauss. On peut calculer la VaR de la position couverte en interpolant la fonction de probabilité cumulative. Pour un α de 1%, le rendement que lui associe la fréquence cumulative serait de -35,8940683%. Ce résultat est obtenu sur une période de 515 jours, soit le nombre d’observations de la simulation. Pour un α de 1%, le rendement associé à la VaR serait d’environ -0,0697% par jour. Calcul de la value at risk par extrapolation linéaire :
f(x)=f(a)+(x-a)((f(b)-f(a))/(b-a))avec b>a
La value at risk est calculée comme suit : (-35,8940683%.)/515=-0,06969722%.
2-La semi-variance comme mesure de risque
La mesure du risque par l’écart-type ne dissocie pas les « mauvais » risques des « bons » risques, en l’occurrence les « downsides » des « upsides » risques. La semi-variance ne prend en compte que les mauvais risques desquels veut-on se couvrir en les minimisant.
〖LPM〗_(M,τ,p)=1/M ∑_(t=1)^M▒〖[MAX(〗 0;τ-(r_(1 )-〖hr〗_2)]^n
M étant le nombre d’observations,
τ est le rendement cible qui sera dans le cas de la semi-variance la moyenne E[r_(1 )-〖hr〗_2 ]= τ
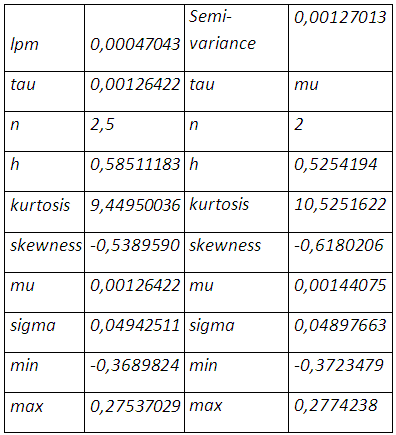
n correspond au degré d’aversion ou de tolérance du risque qui est égal à 2 dans le cadre de la semi-variance. La minimisation de la semi-variance sous Excel, après le choix arbitraire de h=1,nous donne le résultat suivant :
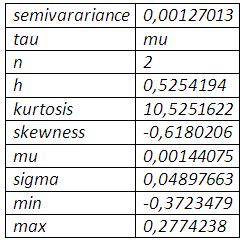
Le bootstrapping des rendements de la position couverte, avec comme taux de couverture 52,54%, exhibe une distribution très asymétrique en faveur des rendements négatifs laissant entendre un avenir risqué.
Le seul mode de cette même distribution enregistre une grande probabilité d’occurrence des rendements nuls qui coïncide à la couverture nette pour ne dire parfaite de la baisse du prix du soja. En calculant la valeur en risque non paramétrique, on peut s’attendre à un rendement de la couverture inférieure à -0,2057% au mois janvier 2012 en cas de scénario défavorable.
3- Low partial moments comme mesure de risque
La moyenne LPM se différencie de la semi-variance par la prise en compte des moments d’ordre supérieur à 2, ce qui en fait une mesure stochastique en portant n ,degré d’aversion ou de tolérance du risque , à une valeur supérieure à 2 et le rendement cible qui peut égal ou non à la moyenne des rendements.
〖LPM〗_(M,τ,p)=1/M ∑_(t=1)^M▒〖[MAX(〗 0;τ-(r_(1 )-〖hr〗_2)]^n
Dans ce cadre nous posons n=2,5, ce qui donne le résultat suivant :
f(1%)=f(0,80%)+(1%-0,80%)((f(2,30%)-f(0,80%))/(2,30%-0,80%))=-32,284485+0,20%*(19,5676509/(1,50%))=-29,6754653%
Value at risk= -0,05762226%
4-la value at risk comme mesure de rsique
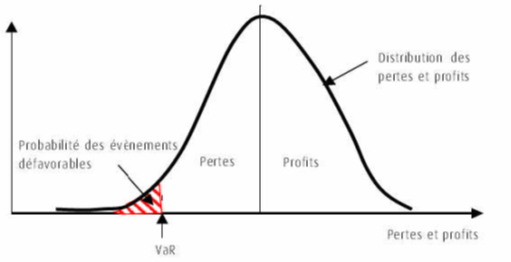
Une autre mesure moins statique et tournée vers le futur est la value at risk. Value at Risk désigne la perte potentielle maximale, à l’intérieur d’un intervalle de confiance donné, supportée par un établissement sur son portefeuille de positions, dans l’hypothèse d’un scénario défavorable de marché sur un horizon déterminé.
Pour une distribution suivant une loi normale, la value at risk est représentée par :
Var= -E[〖r_(1 )-〖hr〗_2]+q〗_α √(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 )
La détermination du taux de couverture optimal, en minimisant le risque qu’est la valeur en risque, consiste à résoudre le programme d’optimisation suivant :
〖Min〗_(h ) (-E[〖r_(1 )-〖hr〗_2]+q〗_α √(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_(2 ) )) s/c h≤1
L’optimisation, sous Excel, donne le résultat suivant :
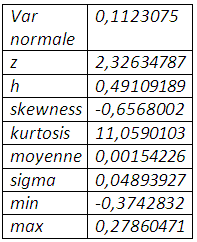
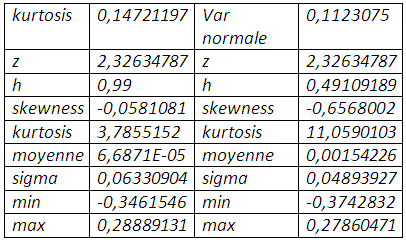
La valeur en risque normale exige un taux de couverture de 49,10%, encore faut-il que l’hypothèse de normalité tienne pour s’y fier. En effet l’excédent de kurtosis, conjugué avec une distribution étalée vers la gauche, conduit à sous-estimer le risque de baisse du prix du soja et par conséquent le taux de couverture qui en découle.
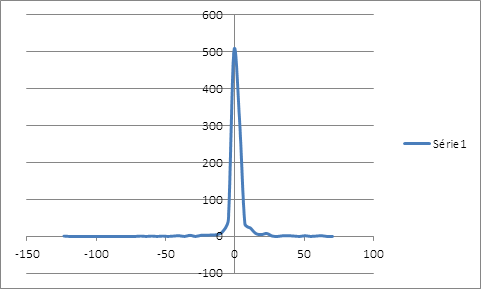
Le ré-échantillonnage des rendements de la position couverte, avec comme taux de couverture 49,10% , montre une distribution qui laisse entendre un avenir risqué avec l’étalement à gauche , même si le seul mode de cette même distribution enregistre une grande probabilité d’occurrence des rendements nuls qui coïncide à la couverture nette pour ne dire parfaite de la baisse du prix du soja. En calculant la valeur en risque non paramétrique, on peut s’attendre à une baisse du prix du soja inférieure à 0,062777% au mois janvier 2012.
5-La valeur en risque conditionnelle
La valeur en risque mesure le risque par la probabilité cumulative. Mais elle comporte plusieurs défauts. D’abord, elle n’est pas une mesure cohérente du risque. La VaR d’un portefeuille de titres n’est pas, dans certains cas, plus faible que la somme des VaR de ses composantes. Elle escamote alors le principe de la diversification, un principe de base en finance. Elle ne tient pas compte de la forme de la distribution des rendements et dès lors ne renseigne guère sur les pertes extrêmes que peut subir un portefeuille.
L’ES mesure la perte qui ne sera pas atteinte en cas de dépassement de la valeur en risque, et reste une mesure cohérente au dépens de la valeur en risque au sens où il respecte la propriété de sous-additivité à laquelle la value at risk fait défaut. L’ES s’établit comme suit :
C’est dans ce contexte qu’a été développée la VaR conditionnelle, soit la CVaR. On peut la définir comme suit :
〖ES〗_α (R_p )=E(R_p⁄R_p <〖Var〗_p)
Dans le cadre de la loi normale, la valeur en risque conditionnelle est identique à :
〖ES〗_α (R_p )=E(R_p⁄R_p <〖Var〗_p)
〖 ES〗_α (R_p )=(〖E(R_p.I〗_(R_p≤〖Var〗_p )))/α
〖 ES〗_α (R_p )=1/α ∫_(-∞)^(〖Var〗_p)▒〖t/σ_(p√2π) e^(-t^2/(2σ_p^2 )) dt〗
〖 ES〗_α (R_p )=1/(ασ_(p√2π) )[-σ_p^2 e^(-t^2/(2σ_p^2 )) ]_(-∞)^(〖Var〗_p )
〖 ES〗_α (R_p )=(σ_p^2)/(ασ_(p√2π) ) e^(-〖〖Var〗_p〗^2/(2σ_p^2 ))
〖 ES〗_α (R_p )=(σ_p^2)/(ασ_(p√2π) ) e^(-(Z_α^2)/2)
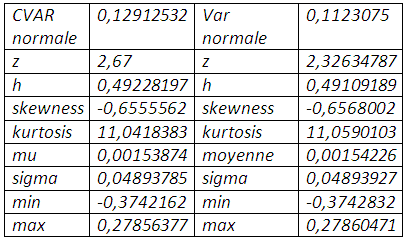
Pour α=0,99 le quantile associé à l’écart-type est égal à 2,67. Par conséquent, la valeur en risque conditionnelle revoit à la hausse le multiple associé à l’écart-type qui passe de 2,33 à 2,67.
La cvar normale augmente sensiblement le taux de couverture, et renvoie aux mêmes interprétations concernant la loi normale. Il en est de même pour le bootstrapping qui affiche une perte de 0,0567518% qui ne sera pas atteinte sur la résultante position dans un mois.
6-value at risk cornish fisher
Les mesures de risque par l’écart-type et la value at risk ne prennent en compte que les deux premiers moments, et ignorent l’asymétrie négative comme positive et le degré d’aplatissement des distributions des rendements. L’expansion cornish fisher nous permet de tenir compte des phénomènes d’étalement de la queue, ou les valeurs extrêmes positives et ou négatives, et des phénomènes d’aplatissement qui enregistrent l’occurrence faible des rendements extrêmes et les grandes déviations par rapport à la moyenne. En effet la valeur en risque Cornish-Fisher est une relation approximative entre les percentiles d’une distribution et ses moments.
Au dire de Stuart et al. (1999), un très grand nombre de distributions que l’on retrouve en Statistique tendent vers la normale quand n (le nombre d’observations) se dirige vers l’infini, mais dans des échantillons de moindre envergure, la distribution normale peut laisser beaucoup à désirer. C’est pourquoi il faut recourir à l’expansion de Cornish-Fisher dans ce cas pour approximer les percentiles d’une distribution. Cette approximation, basée sur la série de Taylor, recourt aux moments d’une distribution qui dévie de la normale pour calculer ses percentiles.
Le rendement de la position résultante étant 〖 R〗_P=r_(1 )-〖hr〗_2 , ses moments d’ordre 3 et 4 s’établissent respectivement comme suit :
〖S〗_P=〖E[r_(1 )-〖hr〗_2]〗^3/〖[√(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 ) ]〗^3
〖K〗_P=〖E[r_(1 )-〖hr〗_2]〗^4/〖[√(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 ) ]〗^4
q_α,le multiple associé jadis à l^’ écart-type pour le calcul de la valeur en risque normale,est ajusté de la façon suivante
〖 W〗_α= q_α+1/65 (〖q_α〗^2-1) S_P+1/24(〖q_α〗^3-3q_α) K_P-1/36(2〖q_α〗^3-5q_α)〖S_P〗^2
Donc la value at risk s’établit comme suit :
Var (R_P=r_(1 )-〖hr〗_2)= -E[r_(1 )-〖hr〗_2 ] + [q_α+1/65 (〖q_α〗^2-1) S_P+1/24(〖q_α〗^3-3q_α) K_P-1/36(2〖q_α〗^3-5q_α)〖S_P〗^2] √(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 )
Le taux de couverture optimal associé peut être obtenu en résolvant le programme d’optimisation suivant :
〖MIN〗_H {-E[r_(1 )-〖hr〗_2 ] + [q_α+1/65 (〖q_α〗^2-1) S_P+1/24(〖q_α〗^3-3q_α) K_P-1/36(2〖q_α〗^3-5q_α)〖S_P〗^2] √(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 )
s/c h≤1
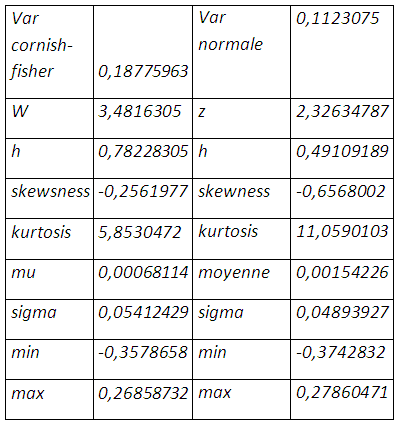
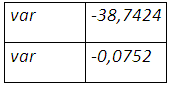
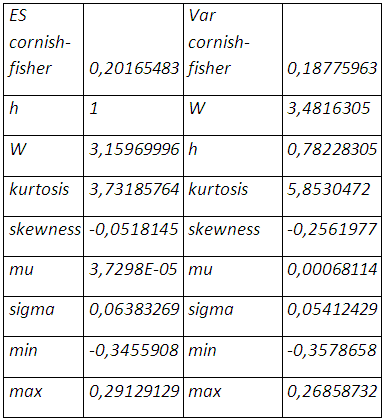
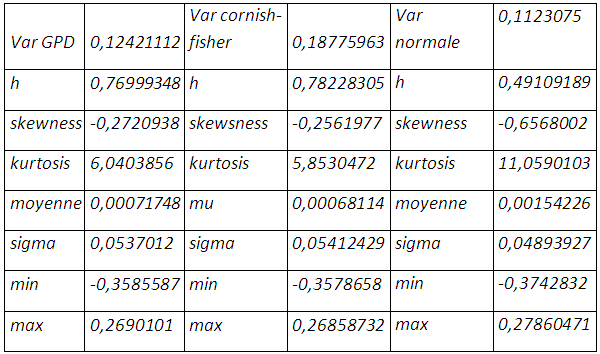
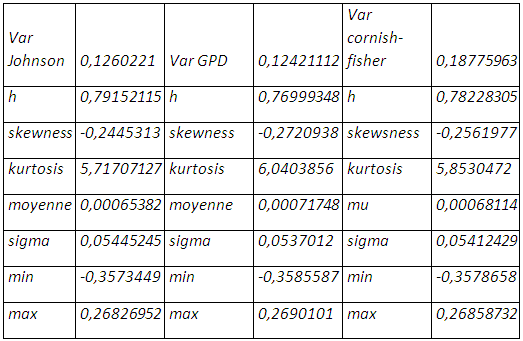
La prise en compte à la fois de l’épaisseur de queue et de l’asymétrie dans la distribution de la position résultante porte le taux de couverture à 78,22%, et une perte de 18,77% qui ne sera pas enregistrée au prochain mois. La value at risk cornish-fisher apporte plus d’optimisme avec une queue moins épaisse même s’il y a étalement à gauche de la distribution et une moyenne des rendements qui tend vers zéro. Bien entendu on une réduction considérable de la négativité de la skewness et de l’épaisseur de queue.
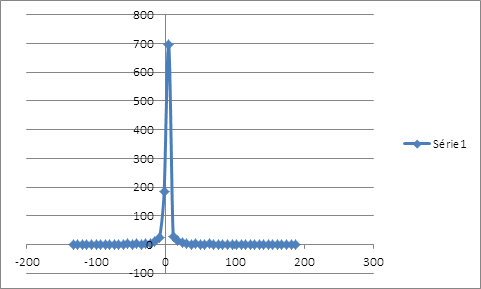
La distribution des rendements de la position couverte, obtenue par ré-échantillonnage, présente un seul mode au niveau des rendements nuls et exhibe plus des gains importants en plus d’une couverture contre la baisse que de pertes, même si les probabilités d’occurrence sont faibles. On a un environnement plus prometteur ou moins risqué que le cas de la normalité. La perte maximale potentielle s’élève à 0,0752% plus grande dans le cas de la loi normale, le risque est moins sous-estimé.
7-Cvar cornish-fisher
Comme la cvar normale, nous évaluons la perte potentielle et le taux de couverture attaché en cas de dépassement de la valeur en risque cornish-fisher.
〖ES〗_p=1/α ∫_(1-α)^1▒〖var(x)dx=-σ_p/α ∫_(1-α)^1▒〖q_p^x dx〗〗
Le calcul sous R donne 〖ES〗_p=-0.207266 si Var (R_P=r_(1 )-〖hr〗_2 )= 0,18775963
La cvar cornish-fisher conduit à une couverture « naïve » portant le taux de couverture à 100% avec une perte maximale possible sur la position résultante de 20,16%.
8-Détermination du taux de couverture dans le cas de non-normalité
8-1-value at risk student
L’épaisseur de queue des rentabilités de la position couverte peut être amortie en recourant à la loi de student qui enregistre un coefficient d’aplatissement de 4 supérieur à celui de la loi normale. Le degré de liberté de la loi de student conditionnellement aux rentabilités Rp peut être estimé par maximum de vraisemblance. Si l’on considère la densité de probabilité f(Rp) et un paramètre θ à estimer, la méthode consiste à déterminer le paramètre qui rend maximale la vraisemblance d’observer ces rendements. La fonction de vraisemblance est donnée par :
L(R_1p,R_2p,…..R_Tp∕θ)=∏_(t=1)^T▒〖f(R_tp∕θ)〗
Il est équivalent de maximiser la log-vraisemblance définie de la façon suivante :
L= ∑_1^T▒ln f(R_tp∕θ) ;v>0
La fonction de densité d’une distribution de student standardisée uni-variée est identique à :
〖f(x)〗_v=(Γ((v+1)/2))/(√π Γ(v/2))×(1+x^2/v )^((-(v+1))/2) ;v>2
Γ(x) est la fonction eulérienne de seconde espèce
Γ(x)=∫_0^(+∞)▒〖e^(-t) t^(x-1 ) dt〗 ;x>0
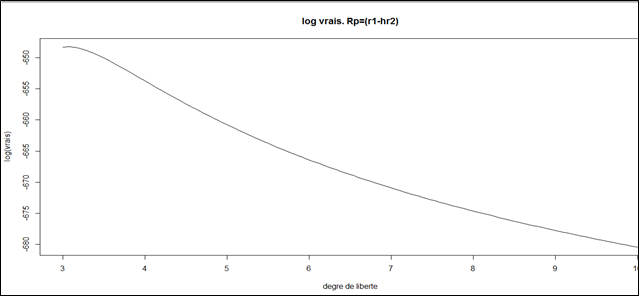
L’estimation du degré de liberté (sous R cf annexe) donne V= 3,06604
Pour une distribution de Student à v degré de liberté la variance vaut : σ^2=1+2/(v-2)
Le quantile utilisé pour calculer la value at risk dans le cas de normalité est révisé de la façon suivante :
〖 q〗_p=q_0,01/√(v/(v-2))
〖 q〗_p=3,444 au lieu de 2,33 qui sous-estime la valeur en risque et par conséquent le taux de couverture qui en résulte.
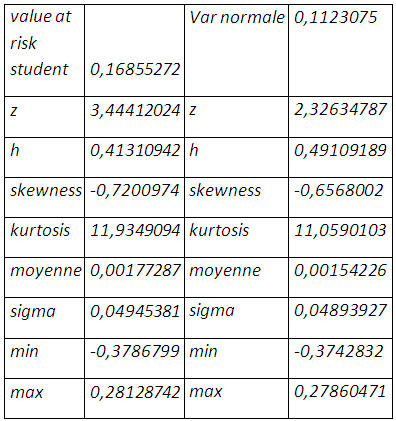
〖varstudent〗_p=q_p √(σ_P^2 )=3,44412024*0,04893927=0,16855272
Le recours de la loi de Student améliore sensiblement l’épaisseur de queue, mais remet en cause une certaine monotonie concernant le taux de couverture qui s’élève à 41,31% plus petit que dans le cas de la loi normale quand bien même une perte potentielle plus grande de 16,85%.
Le bootstrapping des rendements de la position résultante montre une distribution symétrique et un seul mode en faveurs rendements positifs et proches de zéro. Les pertes et gains importants ont la même probabilité faible d’occurrence. Evidemment on est plus proche de la normalité. Et une perte de 0,1094% qui ne sera pas atteinte dans un mois.
8-2: La kurtosis comme mesure de risque
Etant donnée la distribution des rentabilités de la position couverte étalée vers la gauche sous l’hypothèse de normalité, la minimisation du coefficient d’aplatissement peut être considérée comme la minimisation du risque à savoir les pertes extrêmes. Le taux de couverture peut être revu par le programme d’optimisation suivant :
〖Min〗_h 〖K〗_P=〖E[r_(1 )-〖hr〗_2]〗^4/〖[√(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 ) ]〗^4 s/ c h≤1
La résolution du programme donne le résultat suivant :
Minimisation kurtosis
La minimisation de la kurtosis réduit considérablement l’épaisseur de queue et à la fois la négativité de la skewness mais nous conduit à une couverture naïve contrairement à la valeur en risque cornish-fisher.
La distribution, obtenue après ré-échantillonnage, laisse plus d’optimisme avec son étalement vers la droite et son seul et unique mode caractérisé par des rendements nuls, autrement dit une bonne anticipation de l’évolution du prix du soja. La value at risk non paramétrique s’élève à 0,05783% pour le mois suivant.
Les moments d’ordre 3 et 4 peuvent être traités simultanément en vue de minimiser le risque et de trouver le nombre optimal de contrats ; en recourant hormis la value at risk cornish-fisher souffrant de validité, à théorie la théorie des valeurs extrêmes et à la distribution de Johnson.
8-3: Détermination du taux de couverture : approche par la théorie des valeurs extrêmes la distribution de Pareto généralisée
La modélisation des événements extrêmes (ouragan, tremblement de terre ou inondation, crues, crises financières, krachs, chocs pétroliers) est aujourd’hui un champ de recherches particulièrement actif, notamment par l’importance de leurs impacts économiques et sociaux. En particulier, depuis quelques années, on note un intérêt croissant pour l’application de la Théorie des Valeurs Extrêmes (TVE) pour la modélisation de tels événements qui affectent les troisième et quatrième moments. Les domaines d’applications utilisant les modèles de la TVE n’ont cessé de se développer ces dernières années touchant des domaines variés. En hydrologie, domaine dans lequel la prévision des crues par exemple est particulièrement importante [Davison et Smith, 1990 ; Katz, 2002], en assurance dont l’une des préoccupations est la prise en compte des grands sinistres [McNeil et al., 1997 ; Rootzen et Tajvidi, 1997]. Leur introduction en finance [Embrechts et al., 1997 ; Danielsson et de Vries, 1997 ; McNeil, 1998 ; Longin, 1998, 2000 ; Embrechts, 1999 ; Gençay et Selçuk, 2004]) est une réponse immédiate à la remise en cause de l’hypothèse de normalité surtout avec les observations en hautes fréquences. L’abondante littérature et le succès croissant de la TVE dans de nombreux domaines nous a incité à mieux examiner l’apport de cette théorie pour l’analyse des risques encourus sur le marché du soja qui, jadis, a été affecté par le choc pétrolier de 1973 qui a vu une grappe de volatilité où les rendements maximal et minimal se situent.
En appliquant par exemple la TVE au marché nous pouvons répondre aux types de questions suivantes : quelle est la probabilité d’occurrence d’un krach du type de celui de 1973 et son impact sur le prix du soja et bien entendu sur la couverture ?
L’étude et la modélisation des ces extrêmes sont d’importance capitale. En fait la performance d’un investisseur, d’une banque ou d’une entreprise sur une période donnée est souvent le fait de quelques journées exceptionnelles, la plupart des journées d’activité ne contribuant que marginalement au résultat.
Prévoir certains évènements ou comportements, à partir d’une étude des valeurs extrêmes d’une série, est donc un des principaux objectifs pour ceux qui tentent d’appliquer la théorie de ces valeurs. Cette théorie est apparue entre 1920 et 1940, grâce à Fréchet, Fisher et Tippett, Gumbel et Gnedenko. Lorsque l’on modélise le maximum d’un ensemble de variables aléatoires, alors, sous certaines conditions que nous préciserons plus loin, la distribution ne peut appartenir qu’à l’une des trois lois suivantes: Weibull (à support borné), Gumbel et Fréchet (à support non borné). Ces trois lois définissent une famille de distributions statistiques appelée « famille paretienne», dont les applications en sciences sociales sont innombrables et très diverses.
Nous partons de la distribution empirique issue de la valeur en risque empirique. La théorie des valeurs extrêmes englobe deux types de modèles : le modèle des maximums ou minimums d’échantillon d’éléments identiquement distribués, et le modèle qui caractérise les queues de distribution au-delà d’un certain seuil (peak over treseold).
Les distributions de Pareto généralisées permettent de caractériser de façon asymptotique la plupart des queues de distribution de probabilités utilisées en pratique.
Une distribution de Pareto généralisée G_(ξ,β) (x) s’écrit :
G_(ξ,β) (x)=1-(1+ξ x/β )^((-1)/ξ)
Son domaine de définition est {x:1+ξ x/β>0} , ξ est un paramètre de profil qui détermine l^’ épaisseur de queue,β est un paramètre d’échelle
Le k unième n’est défini que pour k<1/ξ
On note L la distribution de perte et F(.) la distribution cumulée de la variable aléatoire L et considérons une valeur s de la partie droite de cette distribution ou le seuil que nous nous fixons et un x >0. On appelle F_S (x) la probabilité pour que L soit inférieur à s+x sachant qu’il est supérieur à s:
F_S (x)=Proba[L≤x+s⁄l>s]=Proba[s<L≤s+x]/Proba[L>s]
F_S (x)=(F(s+x)-F(s))/(1-F(s))
F_S (x) est la probabilité pour que l soit supérieure au seuil d’un montant inférieur à x sachant qu’il dépasse ce seuil. Il s’agit d’une probabilité conditionnelle qui permet de caractériser la distribution inconditionnelle de L.
Il existe un paramètre ξ,et β(s) une fonction dépendant de F tels que F_S (x) converge vers une distribution de Pareto généralisée G_(ξ,β(s)) (x) quand s augmente de sorte que
〖Lim〗_(s∼∞ @x>0) Sup[F_S (x)-G_(ξ,β(s) ) (x)]=0
Les paramètres ξ et β(s) dépendent de la distribution de F, la distribution asymptotique de F_S étant une pareto généralisée sans hypothèse sur la forme de F. au-delà d’un seuil s pour une très large de classe de distributions, F_S (x) peut être assimilé à G_(ξ,β(s)) (x)
pour les paramètres ξ,β qui font l’objet d’estimation. Le paramètre ξ est d’autant élevé que la queue de distribution est épaisse. La fonction de densité est réécrite comme suit :(dG_(ξ,β(s)) (x) )/dx=1/β(1+ξ x/β )^((-(1+ξ))/ξ)
A partir d’un échantillon de n observations de la variable L, on fixe le seuil au niveau du p_S quantile choisi et on considère les valeurs L>s. On ne retient que les n_S observations dépassant le seuil, sous –échantillon à partir duquel la fonction de vraisemblance et la log-vraisemblance sont posées.
∏_(i=1)^(n_S)▒〖1/β(1+ξ (L_i-s)/β )^((-(1+ξ))/ξ) 〗 ; -∑_(i=1)^(n_S)▒((1+ξ))/ξ ln((1+ξ (L_i-s)/β)-nln(β)
Les estimations de ξetβ donne une approximation de la distribution de probabilité conditionnelle F_S (x) :
Proba (L≤l∕L>s)≇G_(ξ,β) (x)=1-(1+ξ x/β )^((-1)/ξ)
La value at risk et l’expected shortfall sont obtenues :
〖Var〗_p=〖Var〗_empirique+ β ̂/ξ ̂ [(n/n_s (1-p)^(-ξ ̂ ))-1] ;
〖ES〗_p=1/(1-ξ ̂ )[〖var〗_p+β ̂ -ξ ̂s]
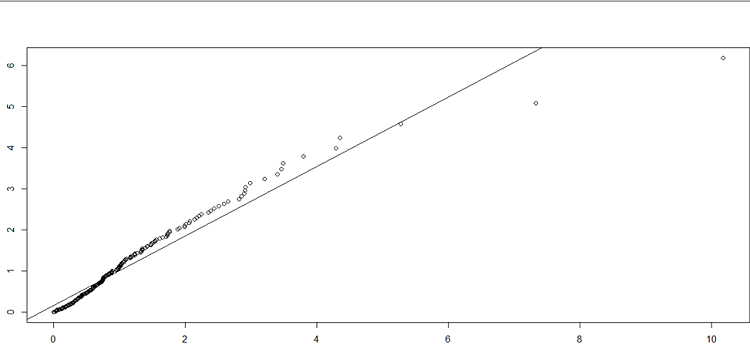
Nous fixons le seuil zéro tout en augmentant le degré d’aversion au risque, ce qui peut paraître restrictif de considérer toute perte comme extrême. En effet nous nous intéressons qu’aux pertes ou la partie gauche de la queue, que l’on rend positives et estime par maximum de log vraisemblance les paramètres selon la distribution de Pareto généralisée (confère logiciel R). Les paramètres d’épaisseur de queue et d’échelle sont identiques à :
ξ ̂=0,10385096 , β ̂=0,002514875
La valeur de ξ ̂ montre la définition des 9 premiers moments k=9,62<1/ξ des rendements de la position résultante issus de l’hypothèse de normalité. La valeur en risque est de 12,42% :
〖Var〗_p=〖Var〗_empirique+ β ̂/ξ ̂ [(n/n_s (1-p)^(-ξ ̂ ))-1]
〖Var〗_p=0,1123075 + 0,01190362=0,12421112
La modélisation de la partie gauche de la distribution renvoie un taux de couverture de 77% sensiblement égal au cas de l’expansion cornish-fisher, avec une réduction de l’épaisseur de queue et de l’asymétrie négative. La perte potentielle maximale s’élève à 12,42% plus petite que celle prévue par l’expansion cornish-fisher.
La proximité de ces performances montre en effet que le prix du soja a été rarement victime de fortes fluctuations sauf le choc pétrolier de 1973 et quelques événements géopolitiques tels la guerre du golf entre autre.
Le bootstrapping confirme la prise en compte unilatérale des pertes, avec une distribution extrêmement étalée à gauche, voire les pires pertes qui peuvent être enregistrées, et d’autre part le plus petit gain et les rendements nuls constituant le seul et unique mode. C’est la plus pessimiste vision du risque que l’on pourrait attendre, la value at risk non-paramétrique étant de 0,1016%.
8-4: La cvar de la distribution générale de Pareto
On peut s’interroger sur la perte et simultanément le taux de couverture, s’il y a un dépassement de la perte prévue par la théorie des valeurs extrêmes.
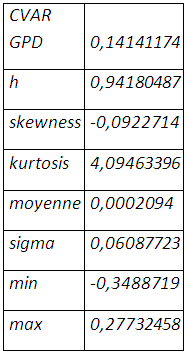
〖 ES〗_p=1/(1-ξ ̂ )[〖var〗_p+β ̂ -ξ ̂s] =〖ES〗_p=0,14141174
« L’extrême » des pertes extrêmes à laquelle on peut s’attendre en un mois est de 14,14% qui est, pourtant, inférieure à celle suggérée par l’expansion de cornish-fisher. La couverture du risque de baisse n’en est pas une naïve, le taux de couverture requis étant 94,18% avec une réduction considérable de l’épaisseur de queue et l’asymétrie sous l’hypothèse de non normalité.
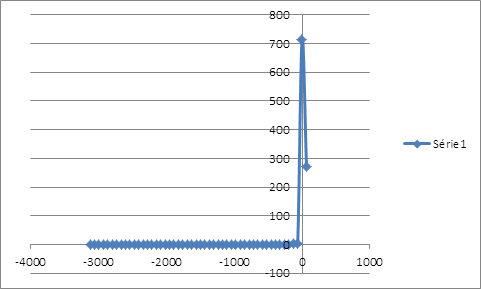
Le ré-échantillonnage montre une distribution loin d’être normale, avec une queue très épaisse située à gauche caractérisant les pires pertes qui peuvent être envisagées. On peut s’attendre à une perte potentielle de 0,1581% dans un horizon d’un mois.
8-5: Distribution de johnson
L’approche de la value at risk par l’expansion cornish- fisher génère des fois des quantiles non-monotones pour certains couples de kurtosis et skewness. En effet, on a des fois des valeurs en risque de 95% plus élevés que celles de 99%.
Le système de Johnson utilise, au même titre que l’expansion cornish-fisher, les 4 premiers moments de la distribution. Il transforme une variable aléatoire z en une variable standard normal y, et s’écrit de façon générale :
y=a+b*g( (z-c)/d )
a,b paramètres de forme ; c le paramètre de location et d un paramètre d’échelle et g appartient à :
ln〖(u)famille lognormale〗
ln(u+√(1+u²))famille unbounded
ln(u/(1-u))famille bounded
u famille normale
La famille à laquelle appartient g est déterminée grâce à l’algorithme de Hill et Al (1976) et consiste à calculer
γ=w^4+2w^3+3w^2-3
Avec w=1/2(8+4k_3^2+4√(4k_3^2+k_4^3 ) 〖 )〗^(1/3) + 1/2 (8+4k_3^2+4√(4k_3^2+k_4^3 ) )^((-1)/3)-1
Avec k_3=skewness et k_(4 ) la kurtosis
Si γ est proche de l kurtosis il s^’ agitde la loi lognormale
Si γ est plus petit la famille unbounded,et la famille bounded si plus petit
Dans notre cas nous cherchons y tel que
y=a+b*g( ([r_(1 )-〖hr〗_2]-c)/d )
La variable aléatoire de Johnson est obtenue par inversion de la fonction :
[r_(1 )-〖hr〗_2 ]=c+d*g^(-1) ( (y-a)/b )
Avec g^(-1)∈
℮^u〖famille lognormale〗
(〖℮^u-〗〖℮^(-u) 〗)/2 famille unbounded
〖1/〗( 1+℮^(-u) ) famille bounded
u famille normale
Le quantile de Johnson est obtenu de la façon suivante :
Φ_J^(-1) (p,a,b,c,d)=c+d*g^(-1) ( (Φ_N^(-1)-a)/b )
Φ_N^(-1) est le quantile d^’ une loi normale standard
La value at risk est obtenue :〖var〗_(J )=-E[r_(1 )-〖hr〗_2 ]+Φ_N^(-1) √(σ_1^2+〖h^2 σ〗_2^2-2hρ_1,2 σ_1 σ_2 )
L’estimation des paramètres (sous R) donne les résultats suivant :
a= 0.08248765; b= 1.248977, c= 0.00529922 et d= 0.03899756
L’ajustement des rendements de la position résultante issus de l’hypothèse de normalité à la distribution de Johnson, accroit le quantile de 2,32 à 2,57 et porte la valeur en risque à 12 ,60%.
Φ_N^(-1)=2,575071268
〖var〗_(J )=0,1260221
Tout comme la distribution générale de Pareto et l’expansion cornish –fisher, l’ajustement à la distribution de Johnson réduit sensiblement plus à la fois l’épaisseur de queue et l’asymétrie négative. Par conséquent le taux de couverture est plus élevé et se chiffre à 79,15%.
Le ré-échantillonnage, sous un taux de couverture de 79,15%, laisse voire un avenir peu risqué de la position résultante avec l’asymétrie en faveur de gains sur la couverture, et une perte potentielle maximale de 0,0719155% sur un mois.
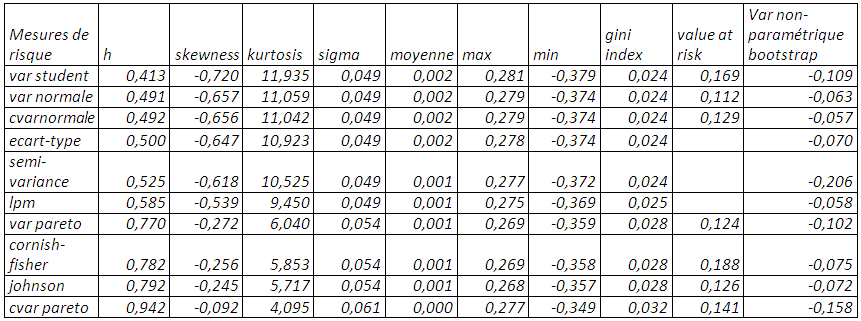
9-L’indice de gini et les mesures de risques
L’indice de gini est calculé pour toutes les couvertures découlant des mesures de risques. Le classement des indices de gini pour chaque taux de couverture, étant plus il est proche de zéro et moins on est en présence de risque, conduit à retenir le taux de couverture induit par la valeur en risque suivant la loi de student en excluant les couvertures dites « naïves ».
Mesure d’inégalité de prédilection, le coefficient de gini comme mesure de risque semble maximiser les moments d’ordre 1 et 4 ou la moyenne et le coefficient d’aplatissement de notre série de rendements.
La sélection du taux de couverture issu de la valeur en risque student peut être motivé également par la forme et les caractéristiques de la distribution obtenue par ré-échantillonnage. Rappelons que la distribution est symétrique avec un coefficient d’asymétrie nul très proche de la loi normale.
Retour au menu : La couverture des produits agricoles sur les marchés à terme : Cas du soja