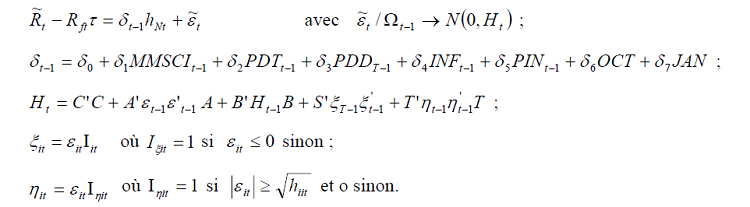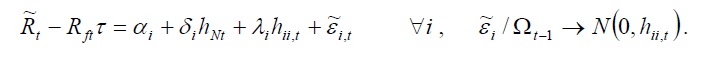3.3.1 MEDAF conditionnel
On a déjà pour acquis que MEDAF conditionnel appliqué à l’international présuppose que l’anticipation de l’excès de rentabilité d’un actif financier est reliée linéairement à la covariance conditionnelle entre cet actif et le portefeuille de marché. Le modèle que nous appliquons est composé des équations suivantes :
Un MEDAFI valide suppose implicitement que les marchés étudiés ne sont pas segmentés. Dans ce cas le prix de risque de covariance est positif et commun à tous les marchés c’est-à-dire :
Pour faire le test de MEDAFI nous analysons deux cas de figure du modèle :
– Modèle à prix de risque de covariance constant ;
– Modèle à prix de risque variable dans le temps.
3.3.2 Prix de risque constant
Dans cette partie, nous considérons que le prix de risque du marché mondial est constant et unique pour tous les portefeuilles nationaux y compris au portefeuille du marché mondial. Cela veut dire que même si les composantes du prix du risque fluctuent suivant les dates, la tangente de la droite de marché des capitaux reste constante. De nombreuses études sur le MEDAFI international ont observé cette restriction. Dans ce cadre nous citons les travaux de Giovannini et Jorion (1989), Karolyi et Stulez (1992) et De Santis et Gérard (1997,1998).
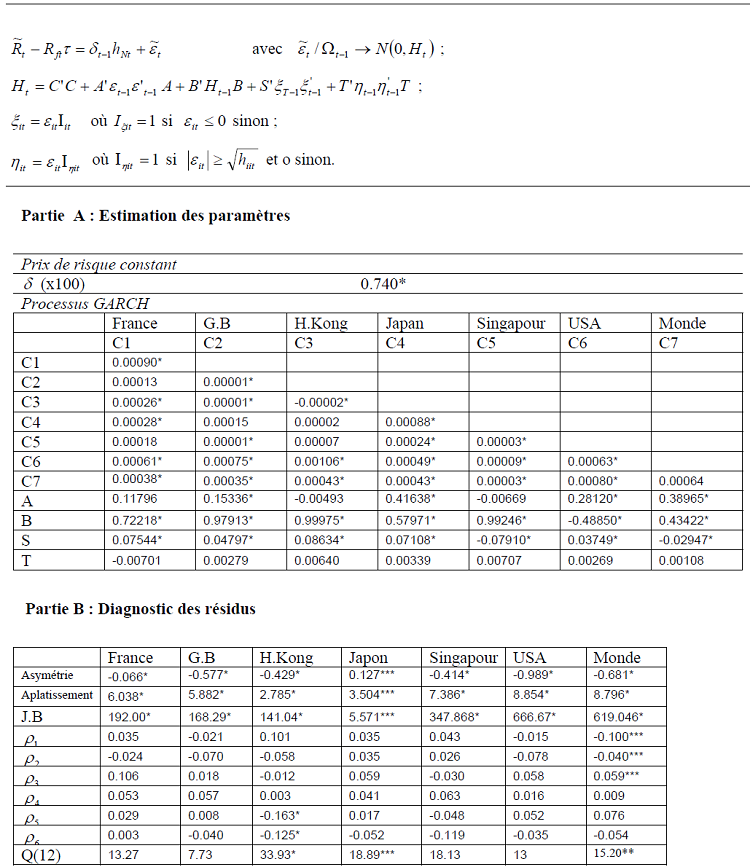
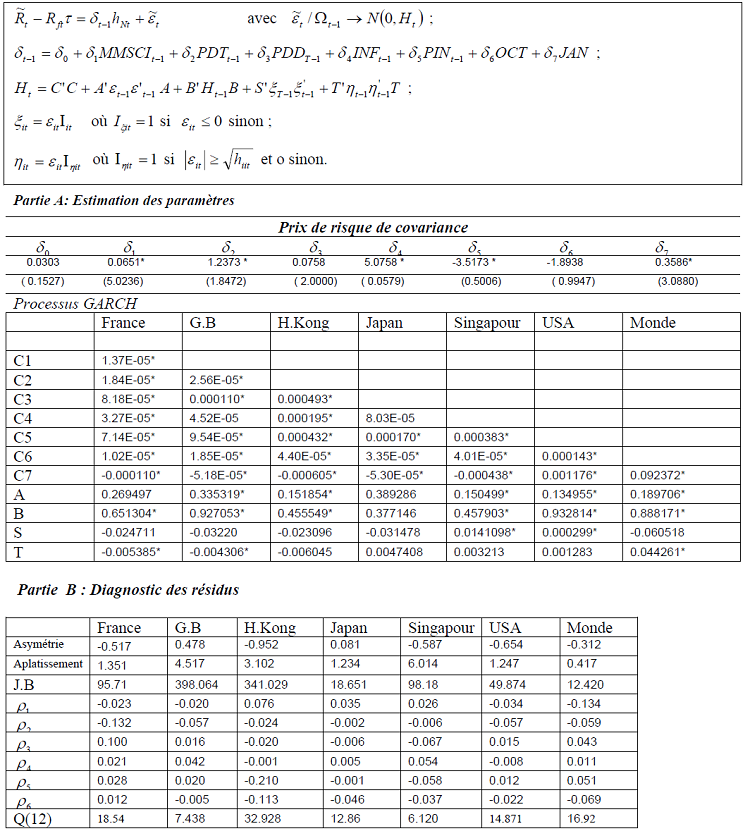
Tableau 9 : Résultats de l’estimation sous Eviews du MEDAF conditionnel avec prix de risque de covariance constant
* significatif au seuil de 1%
** significatif au seuil de 5%
*** significatif au seuil de 10%
JB. test de normalité de Jaque-Bera
Q(12) :test de Ljung-Box d’ordre 12
Ainsi le prix de risque de covariance moyen est estimé à 0.740. Il est significatif au seuil 1% ce qui raisonnable en valeur et en signe.
La partie A donne une idée sur la configuration des moments conditionnels. Les coefficients a et b du processus GARCH sont dans leur majorité positifs et significatifs à 1%. Les paramètres estimés remplissent les conditions de la stationnarité puisque selon le théorème de Bollerslev (1986), le processus BEKK est stationnaire si aiaj + bibj+ < 1 ∀i,j. Les valeurs estimées du vecteur B qui relient les seconds moments à leurs valeurs historiques sont de loin supérieures à ceux du vecteur A qui relient quant à eux les seconds moments aux innovations passées, ce qui semble t- il dégage une forte persistance. Nos résultats sont en harmonie avec les études antérieurs employant le processus GARCH.
Notre modèle présente l’avantage d’autoriser aux seconds moments conditionnels de répondre différemment aux chocs et leur importance. Dans ce cadre nous rejoignons Engle et NG (1993) qui attestent qu’un choc négatif a plus d’impact sur la volatilité qu’un choc positif. D’ailleurs, les coefficients significatifs du vecteur S témoignent que la variance conditionnelle est plus importante que le cas d’un choc négatif pour presque tous les marchés. Ce qui a pour conséquence l’augmentation des variances conditionnelles entre ces marchés à la suite d’un choc négatif. Curieusement, les coefficients du vecteur T ne sont pas significatifs. Il paraît qu’un choc commun négatif ou positif n’a pas d’impact sur les covariances conditionnelles.
Le compartiment B renferme des tests sur les résidus dans le but de porter un jugement sur la performance du modèle estimé. Hormis la France, le coefficient d’asymétrie est significatif pour tous les marchés. Le coefficient d’aplatissement quant à lui est positif et significatif pour tous les pays. Ainsi, l’hypothèse de la normalité est rejetée pour l’intégrité des marchés ce qui justifie le recours à la technique du quasi-maximum de vraisemblance.
Enfin nous avons mené le test Q de Ljung-Box pour chaque série de résidus, l’hypothèse d’absence d’autocorrélation d’ordre 12 est rejetée pour tous les marchés, exception faite de la France, des États–Unis et de la Grande Bretagne.
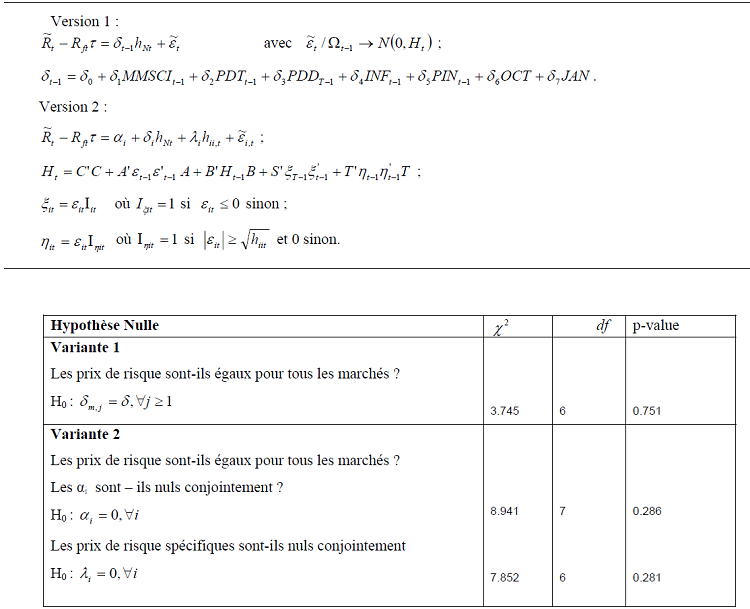
Pour les tests de spécification afférents au modèle avec prix de risque constant, nous avons testé deux variantes du modèle de base. Dans la première variante, nous admettons la possibilité que les marchés soient segmentés, ce qui veut dire que le prix de risque peut changer d’un pays à l’autre. Si les prix de risque sont tous égaux l’hypothèse de l’intégration financière est admise :
La seconde variante est un modèle d’intégration partielle où les primes de risque sont déterminées par un ensemble de facteurs domestiques et globaux. Ce faisant, le risque spécifique à chaque marché, mesuré par la variance conditionnelle, est introduit dans le modèle. Par analogie aux travaux antérieurs nous introduisons une constante spécifique à chaque pays pour capter les autres formes d’intégration non intégrées dans le modèle de base. L’hypothèse nulle d’intégration financière parfaite implique la nullité de la constante et du prix de risque de variance et l’égalité des prix pour tous les marchés.
Ces hypothèses sont testées par le test de Wald à partir des estimations des modèles par la méthode du quasi-maximum de vraisemblance.
Les résultats de test de Wald :
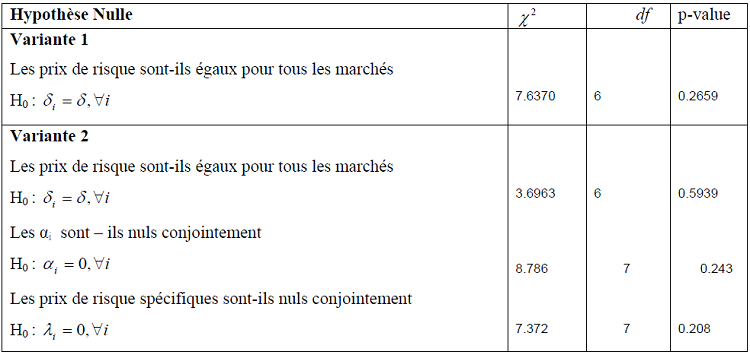
– Ne permettent pas de rejeter l’hypothèse d’égalité des prix de risque de covariance pour tous les marchés ;
– Les hypothèses de constantes et de prix de risque de variance conditionnelle nuls, sont admises à tous les niveaux de significativité conventionnels.
Tableau 10 : Tests de spécification du MEDAF à prix de risque constant
Ces résultats sont cohérents et confortent notre démarche car ils sont conformes avec les conclusions de De Santis et Gérard (1997) qui soutiennent le MEDAF international conditionnel. Cependant, le modèle en question présente l’inconvénient de supposer la constance de prix de risque de covariance, ce qui n’est pas réaliste. En effet, si les excédents de rentabilité sont plus que leurs covariances conditionnelles avec le portefeuille de marché, le schéma du modèle du prix de risque constant apparaît inapte à expliquer la dynamique de la prime de risque. Raison pour laquelle nous admettons que les occasions de placements dans les différents pays sont variables dans le temps. De cette manière, on peut travailler avec des prix de risque de covariance variables suivant les dates.
3.3.3 Prix de risque variable dans le temps
Afin d’opérationnaliser la version conditionnelle du MEDAF à prix de risque de covariance variable dans le temps, nous utilisons un ensemble de variables informationnelles. Il serait impossible d’identifier tous les déterminants de la dynamique du prix du risque. Seul le recours à l’analyse empirique peut permettre d’identifier ces facteurs. Ainsi, le paramétrage de la dynamique du prix du risque peut être critiqué pour son caractère parfaitement qualifié. L’exploration de la littérature financière y afférente, nous renseigne que la plupart des études empiriques supposent que le prix de risque dépend linéairement d’un petit nombre de facteurs. Dans ce travail, nous utilisons le vecteur informationnel Z décrit précédemment.
Tableau 11 : Estimation avec la méthode du quasi-maximum de vraisemblance du MEDAFI avec prix de risque de covariance variable
* significatif au seuil de 1%
** significatif au seuil de 5%
*** significatif au seuil de 10%
JB. test de normalité de Jaque-Bera
Q(12) :test de Ljung-Box d’ordre 12
Le tableau précèdent résume les résultats de l’estimation du MEDAF conditionnel avec prix de risque variable dans le temps par la méthode de quasi-maximum de vraisemblance. On remarque bien que la configuration des seconds moments conditionnels a changé légèrement. Les conditions requises pour la stationnarité sont vérifiées. Les éléments des matrices A et B sont significatifs et positifs. On constate, également que comme dans le cas du modèle à prix de risque constant, les valeurs estimées des coefficients b sont nettement supérieures à ceux de a, ce qui semble indiquer une forte persistance.
Les éléments significatifs du vecteur S sont positifs et ceux du vecteur T sont tous négatifs, ce qui est en harmonie avec les résultats antérieurs.
Quant au prix de risque de covariance moyen il est égal à environ 0.189 et significatif à 1%. C’est le portefeuille de marché mondial qui détermine la dynamique du prix de risque de covariance. La prime de terme et dans une faible mesure, l’effet de janvier y contribuent également. Le coefficient rattaché au crash d’octobre est significativement négatif. En définitive, on peut dire que les signes des variables de vecteur informationnel Z sont plausibles et justifiés économiquement ce qui est d’ailleurs conforme aux études antérieures.
Le MEDAF conditionnel avec prix de risque constant, présente l’insuffisance de ne pouvoir capter les covariances conditionnelles qui reflètent les variations des excès de rentabilités notamment pour les deux marchés émergents qui font partie de ce travail. Le diagnostic des résidus confirme ce constat.
L’hypothèse de normalité est rejetée pour toutes les séries des résidus. Néanmoins, les coefficients d’asymétrie et d’aplatissement ont diminué dans la plupart des cas.
Le tableau 12 présente les résultats de test de spécification relatifs au MEDAF international conditionnel avec prix de risque variable suivant les dates. Toutes les hypothèses sont testées par le test robuste de Wald à partir des estimations des modèles par la méthode du quasi-maximum de vraisemblance.
L’hypothèse de la constance du prix de risque de covariance est rejetée à tous les niveaux de significativité conventionnels. Cependant, le test de Wald ne permet pas de rejeter ni l’hypothèse de nullité jointe des α i ni celle de nullité jointe du prix de risque spécifique aux pays.
Tableau 12 : Tests de spécification du MEDAF à prix de risque variable
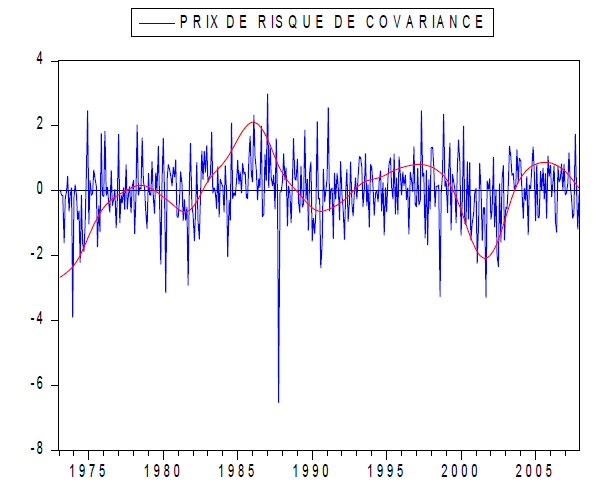
Figure 7 : Prix de risque de covariance
La figure 7 présente l’évolution du prix du risque de covariance estimé ainsi que la série filtré par la technique d’Hodrick et Pescott (1996), c’est une technique qui permet de séparer les mouvements de court terme du mouvement de long terme. On remarque bien que la série filtrée atteint son point le plus bas en juin 1973 (-0.235). Elle augmente entre 1974 et 1978 pour atteindre un seuil d’environ 0.70 en juin 1987.Le prix de risque de covariance entame une tendance à la baisse entre 1978 et 1982 pour arriver à une valeur minimal de -0.252 en 1981. Le prix de risque s’accroît ensuite pour atteindre sa valeur maximale en 1986. Il diminue en octobre 987 mais demeure toujours positive. La série reste un peu stable durant les années 90. Vers la fin des années 90 le prix de risque amorce une phase baissière jusqu’à l’an 2002, il reprend son mouvement haussier pour décroître à partir de 2005.
Les périodes de prix de risque négatif sont associées aux crises pétrolières de 1973-1974, aux réformes de politique monétaire de 1979-1982 et aux dernières crises des marchés émergents.
Page suivante : 3.4 Diversification internationale
Retour au menu : INTEGRATION FINANCIÈRE ET DIVERSIFICATION INTERNATIONALE