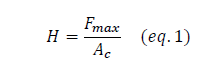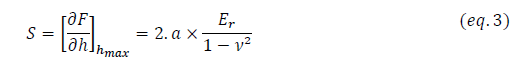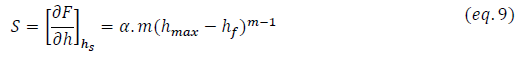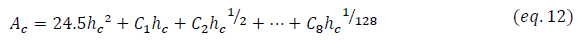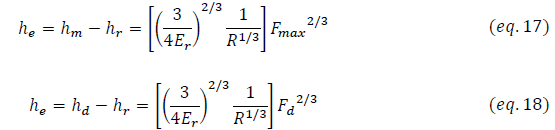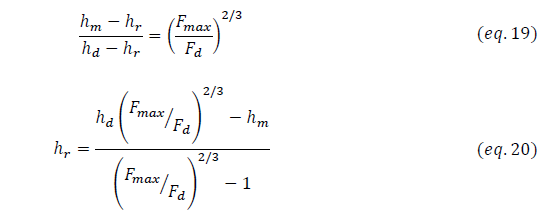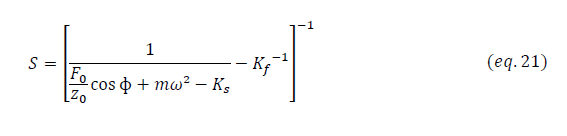III.1 Introduction
Les dépôts PVD sont appliqués souvent pour améliorer la résistance à l’usure et la tenue en service des composants mécaniques. Leur utilisation est donc tributaire de leur niveau de performance.
Le carbure de tungstène est un matériau largement utilisé dans l’ingénierie de précision dû à ces excellentes propriétés mécaniques, sa résistance à l’usure et sa stabilité thermique. D’ailleurs, les revêtements en carbure de tungstène présentent un grand intérêt industriel. Nous sommes alors amenés à caractériser les propriétés mécaniques de ces couches, particulièrement leur dureté et leur module d’élasticité.
Dans ce chapitre, nous introduisons la technique de nanoindentation et la méthodologie d’évaluation de la dureté et du module d’élasticité. Nous présentons les modèles d’interprétations des données issues de cet essai en énumérant les limitations y liées, en particulier ceux de Doener et Nix, d’Oliver et Pharr, et de Field et Swain. Nous abordons ensuite, le mode d’indentation dynamique qui offre plusieurs avantages pour la caractérisation mécanique des couches minces en particulier. Nous utilisons cette technique, à l’aide de deux différents nanoindenteurs afin d’évaluer, la dureté et le module de Young du revêtement étudié, et la sensibilité de l’indentation instrumenté.
III.2 La nanoindentation
Lors de la mesure des caractéristiques mécaniques des dépôts, si la charge appliquée sur l’indenteur est trop importante, les valeurs obtenues sont biaisées par la déformation du substrat. Pour limiter ce phénomène, l’enfoncement maximal de l’indenteur doit être petit par rapport à l’épaisseur du dépôt.
La technique d’indentation instrumentée inventée au cours des années 1980 permet de pallier cette limitation en appliquant des charges de l’ordre de dizaine de micronewtons (μN) pour des profondeurs comprises entre quelques dizaines de nanomètres (nm) et quelques micromètres (μm). La nanoindentation offre une large gamme d’applications pour la caractérisation mécanique des matériaux : dureté, module de Young, fluage, adhérence, etc. La dureté et le module de Young sont les propriétés les plus étudiées.
III.2.1 Principe
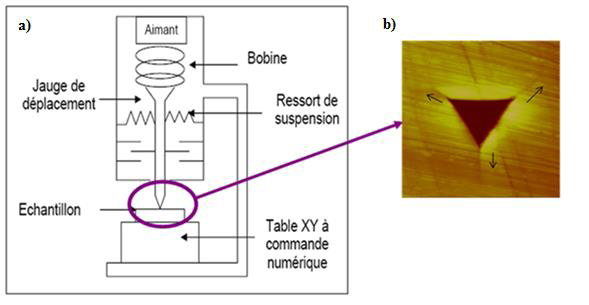
Tout en gardant le principe traditionnel d’indentation, l’essai de nanoindentation consiste, à enfoncer sur la surface d’un échantillon, une pointe (généralement en diamant) supposée indéformable et qui peut avoir différentes formes géométriques.
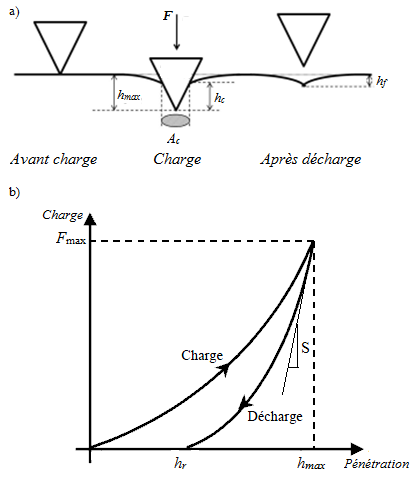
Figure III.1. a) Schéma du système de nanoindentation, b) empreinte d’indenteur Berkovich.
Les géométries d’indenteur les plus répandues dans les essais de nanoindentation sont la pointe de type Berkovich et de type Vickers. Cependant, la pointe Berkovich présente un avantage dû à la possibilité d’avoir un rayon de courbure très petit du fait de l’existence de seulement trois arêtes.
Figure III.2. a) Représentation schématique de la section d’une indentation, b) Courbe d’indentation typique.
Le nanoindenteur suit continuellement l’évolution de l’enfoncement de la pointe avec la charge d’indentation au cours des phases de charge et de décharge afin d’observer la réponse plastique et élastique du matériau. Le résultat est une courbe charge-profondeur présentant le cycle charge-décharge appliqué (figure III.2.b).
En fait, il existe deux modes de fonctionnement d’un essai d’indentation : en contrôle de force ou en contrôle de déplacement de l’indenteur. Le choix dépend du comportement mécanique et de l’épaisseur de la couche étudiée. Généralement pour les couches minces, la profondeur d’enfoncement ne dépasse pas 10 % de l’épaisseur du dépôt.
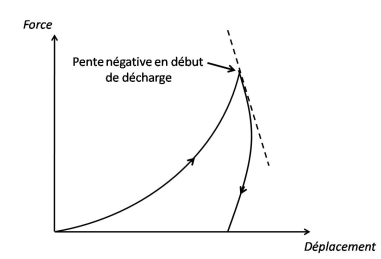
La courbe d’indentation présente deux parties distinctes. La première partie de charge correspond à l’enfoncement de la pointe d’indentation jusqu’à la pénétration maximale hmax, représentant à la fois les contributions élastique et plastique et ne peut donc pas être exploitée directement pour le calcul de la dureté. La deuxième partie de décharge représente le retrait de la pointe d’indentation en laissant une empreinte résiduelle de profondeur hf. La courbe de décharge représente la restitution élastique du matériau dont la pente initiale (au début de la décharge) présente la raideur de contact S.
III.3 Détermination de la dureté et du module d’élasticité par nanoindentation
La détermination des propriétés mécaniques par indentation était le point d’intérêt de plusieurs chercheurs pendant des décennies. La dureté d’un matériau a été définie par Meyer comme étant la résistance à la déformation plastique [78]. Elle s’exprime alors par le rapport entre la force maximale appliquée par l’indenteur et l’aire déformée plastiquement. Cette dernière présente éventuellement l’aire de contact, entre l’indenteur et le matériau, projetée sur la surface; une entité qui n’était pas exploitable dans les essais classiques de dureté. Oliver et Pharr [89,90] ont établi un modèle analytique qu’on détaillera dans le paragraphe 4.2 pour la mesure de dureté par l’indentation instrumentée en exploitant cette grandeur. Ils définissent donc la dureté par l’équation suivante :
Où Fmax est la force maximale appliquée et Ac est l’aire de contact projetée.
L’analyse du comportement élastique entre deux solides en contact établie par Hertz représente la base de tous les travaux menés sur la caractérisation du comportement élastique des matériaux par indentation. La relation établie par Hertz [79-81] déterminant le module d’élasticité équivalent de deux solides en contact, a été utilisé par Sneddon [82] pour définir un module effectif, ou module réduit Er, qui prend en compte à la fois, la déformation élastique de l’échantillon et de l’indenteur. Le module d’élasticité équivalent s’exprime par la relation suivante :
Où Ei et E sont respectivement les modules de Young de la pointe d’indentation et du matériau, tandis que νi et ν sont leurs coefficients de Poisson.
En considérant que la décharge infinitésimale d’un indenteur axisymétrique quelconque est décrite par le même comportement que la décharge d’un indenteur sphérique de même aire de contact, Sneddon [82] lie le module d’élasticité équivalent, à la raideur de contact S déterminée expérimentalement de la courbe de décharge, par l’équation suivante :
Où a est le rayon de la zone de contact, qui peut être exprimé par l’équation (4) :
Avec Ac : l’aire de contact projetée sur la surface indiquée dans la figure IVI.2.a.
Les travaux de Bulychev et al [83-85] montrent que cette relation peut être appliquée pour n’importe quel type d’indenteur (Sphère, Vickers, Berkovich….) en introduisant un facteur correctif β qui prend en compte le caractère non axisymétrique des indenteurs autres que sphériques ou cylindriques plats. Ainsi, ils proposent l’équation suivante :
Où β est égale à 1 pour une symétrie de révolution, 1,034 pour une symétrie triangulaire et 1,012 pour une symétrie carrée.
Les équations ci-dessus montrent que pour déterminer la dureté et le module de Young d’un matériau ou d’un dépôt, il est indispensable de connaitre les deux paramètres clés qui sont la raideur de contact S et l’aire de contact projetée Ac. Cependant, l’aire de contact entre l’indenteur et le matériau à indenter peut être définie comme étant une fonction d’aire qui dépend de la hauteur de contact entre le matériau et la pointe notée hc. Cette dernière est une caractéristique géométrique de la pointe.
Pour des pointes de types Vickers et Berkovich, la relation géométrique A=f(hc) est très proche et donnée par (détails dans annexe 1) :
Plusieurs modèles d’analyse des courbes d’indentation ont été développés pour déterminer l’aire de contact Ac, par conséquent la dureté et le module d’élasticité. Leur objectif principal consiste à pouvoir séparer les contributions élastiques de la réponse du système couche-substrat afin de rendre possible le traitement de la partie élastique à l’aide des équations analytiques fournies par Hertz [79-81] et Sneddon [82]. La validité des résultats pour la dureté et le module de Young dépendent largement de la procédure utilisée. Ainsi dans la partie suivante, trois méthodes d’analyse des courbes d’indentation seront présentées : la méthode de Doerner et Nix, ainsi que les plus récentes en occurrence la méthode de Oliver et Pharr et celle de Field et Swain.
III.4 Modèles d’analyse des courbes d’indentations
III.4.1 Modèle de Doener et Nix
Au début des années 60, Sneddon [82] a développé un modèle permettant l’analyse des courbes d’indentation. Son modèle décrit par l’équation (7), permet d’établir la relation entre la force appliquée et la profondeur d’enfoncement lors de l’indentation.
F étant la force appliquée sur la pointe d’indentation, h est son déplacement total, α est une constante qui dépend du matériau et m est aussi une constante qui est fonction de la géométrie de l’indenteur : m=1 pour un cylindre plat, m=1,5 pour une sphère et m=2 pour un cône.
En se basant sur l’étude de Sneddon, Doener et Nix [87] ont négligé l’effet de géométrie de la pointe d’indentation et ont supposé que le contact d’indentation peut être assimilé comme étant un espace axisymétrique (cas d’indenteur cylindrique plat) durant toute la décharge. Dans ce cas, l’aire de contact reste constante au début de la décharge. La courbe de décharge est ainsi supposée linéaire (m=1). L’intersection de la tangente à force maximale avec l’axe horizontal donne la profondeur de contact hc. L’aire de contact est alors déterminée à partir de l’analyse directe de la courbe d’indentation sans recours à la mesure optique de l’empreinte résiduelle.
Néanmoins, cette méthode présente des imprécisions puisque la décharge n’est pas totalement linéaire pour tout type de matériaux. En outre, la géométrie de la pointe d’indentation a un effet notable dans l’analyse de contact.
III.4.2 Modèle d’Oliver et Pharr
La méthode développée par Oliver et Pharr en 1992 [89] puis revue en 2003 [90], est le modèle d’interprétation de la courbe d’indentation le plus rigoureux actuellement, et qui fait aujourd’hui référence pour tous les appareillages de nanoindentation.
À partir des expériences d’indentation réalisées sur six matériaux différents, Oliver et Pharr [89] ont montré que l’hypothèse de la linéarité du début de la courbe de décharge n’est pas satisfaite. En se référant aux travaux de Sneddon, ils suggèrent un modèle prenant en compte les caractéristiques géométriques du contact entre l’indenteur et le matériau. Leur modèle propose de relier la force à la profondeur de pénétration par une loi de puissance (équation 8) pour mieux représenter la courbe de décharge et déterminer ainsi la raideur de contact S.
Ainsi, un simple calcul par dérivation permet d’évaluer la raideur de contact au point de profondeur maximale :
Avec h, hf et hmax sont respectivement la profondeur, la profondeur résiduelle, et la profondeur maximale d’indentation. α et m sont des constantes déterminées par ajustement en fonction des données expérimentales où l’exposant m varie entre 1,2 et 1,6 en fonction de la géométrie de l’indenteur.
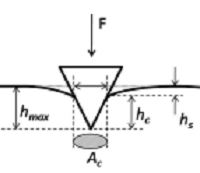
Connaissant la raideur de contact, il ne reste que la détermination de l’aire de contact pour l’évaluation de la dureté et le module de Young. Oliver et Pharr ont pris en compte dans leur modèle, la déflexion élastique de la surface sous l’enfoncement de l’indenteur. Une modélisation de la déflexion élastique est illustrée dans la figure III.3.
De ce fait, la profondeur de contact hc peut être déterminée à partir de la courbe d’indentation par la relation suivante :
Où hs est la profondeur traduite par la déflexion élastique comme indique la figure IV.3.
Figure III.3. Modélisation du contact d’après Oliver et Pharr.
Puisque hmax est mesurable expérimentalement, la clé de l’analyse devient hs. Oliver et Pharr [89,90] supposent que la surface de déflexion qui est à la fois à la limite de contact est suffisamment loin de la zone plastique, d’où la déflexion hs peut être considérée comme purement élastique. En reprenant les travaux de Sneddon [82] sur la déflexion élastique d’une surface sous un indenteur conique et sphérique, ils aboutissent à une relation entre la profondeur hs, la force maximale, la raideur de contact et la géométrie de la pointe d’indentation :
Avec ε un paramètre traduisant la géométrie de la pointe : ε = 0.72 pour un cône, pour une sphère ε = 0.75 et ε = 1 pour un poinçon plat.
En déterminant la profondeur hs, il est donc possible d’évaluer, à partir des données expérimentales, l’aire et la rigidité du contact entre la pointe d’indentation et le matériau indenté.
Par ailleurs, la détermination de l’aire de contact nécessite une prise en considération de l’imperfection géométrique de l’indenteur due à son usure. Oliver et Pharr proposent des corrections permettant de mieux évaluer les données issues de l’essai de nanoindentation en introduisant des coefficients prenant en compte l’imperfection même minime de la pointe d’indentation dans l’équation 6. L’aire de contact devient donc exprimée par l’équation suivante :
Les coefficients C1,…, C8 sont déterminés par une calibration à partir d’une série d’expériences d’indentation réalisée sur un matériau donné.
De nombreuses études récentes portent une attention particulière à l’évaluation du facteur correctif β de la relation (eq.5) [96,97]. Oliver et Pharr [90] proposent des valeurs tirées des travaux de King [91] où elles sont évaluées par simulation numérique. Leurs recherches montent que la valeur du coefficient géométrique β dépend non seulement de la géométrie de la pointe, mais aussi du coefficient de Poisson du matériau indenté. D’après leur publication [90], β est compris entre 1,02 et 1,08 pour un indenteur de type Berkovich.
Le module de Young est ainsi explicité d’une façon précise et directe à l’aide de la méthode d’Oliver et Pharr. Quant à la dureté mesurée par cette méthode, elle prend en compte les déformations élastiques et plastiques à force maximale.
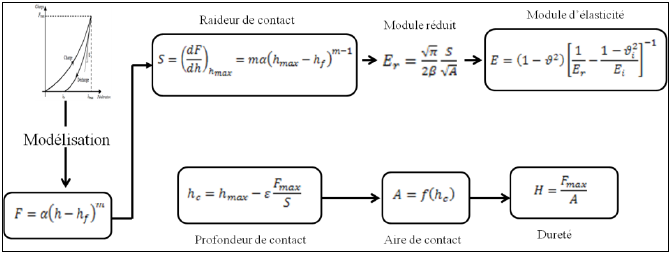
La figure III.4 retrace les principales étapes de la détermination de la dureté et du module de Young d’un matériau en utilisant le modèle d’interprétation développé par Oliver et Pharr.
Figure III.4. Modélisation d’Oliver et Pharr.
III.4.3 Limitation de la méthode d’Oliver et Pharr
L’importante limitation de cette méthode est que l’analyse est faite à une profondeur fixe. Si l’on cherche à obtenir des mesures à différentes profondeurs, il est nécessaire de réaliser plusieurs essais.
Figure III.5. Représentation schématique de la sous-estimation de l’aire de contact en présence de, a) sink-in, b) pile-up.
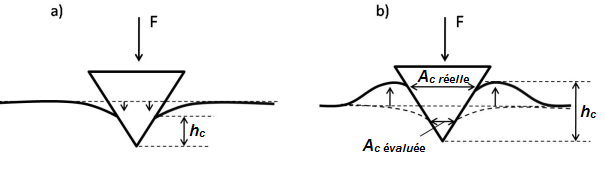
En outre, Oliver et Pharr évaluent l’aire de contact entre l’indenteur et le matériau indenté en considérant que ce dernier subit une déflexion élastique comme indique la figure III.5.a. Ce comportement pris en considération est appelé phénomène sink-in. Alors que certains matériaux, particulièrement les matériaux mous, lorsqu’ils sont indentés, révèlent une accumulation de matière sur les bords de l’empreinte, qu’on appelle bourrelet [92] : c’est le phénomène de pile-up. Ainsi, l’aire de contact est sous-évaluée comme il est expliqué dans la figure III.5.b. Cela induit une surestimation de la valeur du module d’élasticité de la couche et surtout de sa dureté qui est proportionnelle à ce paramètre.
Le problème qui s’oppose à la prise en considération de ce phénomène par le modèle d’Oliver et Pharr, est que la quantité de pile-up ou de sink-in dépend des caractéristiques intrinsèques du matériau, donc sans aucune information sur ces caractéristiques le problème ne peut pas être résolu. Une simulation par la méthode des éléments finis du pile-up de différents matériaux élastoplastiques a été faite par Cheng et al [94]. Leur méthode consiste à évaluer la quantité de travail de l’indentation sans impliquer l’aire de contact dans le calcul direct. Ils ont trouvé que le travail irréversible, lié à la déformation plastique, dépend du rapport Er/H. Mais, cette méthode n’est pas justifiée expérimentalement et souffre de plusieurs insuffisances pour le cas des matériaux à haute élasticité. Bolshakov et Pharr [95] ont montré par la méthode des éléments finis que si le retour élastique reste supérieur à 30 % ou si un phénomène non négligeable d’écrouissage a lieu, le phénomène de pile-up reste négligeable.
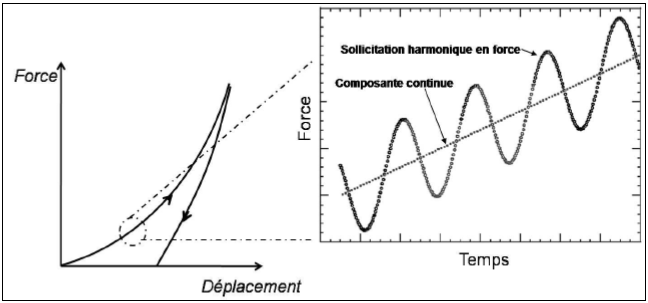
Certains matériaux en particulier les polymères présentent un effet de fluage lors de l’essai d’indentation. Ce comportement est mis en évidence sur la courbe d’indentation comme étant une augmentation du déplacement pour une diminution de la force lors du début de la décharge (figure III.6) [96]. Le fluage au début de la décharge entraine des erreurs sur l’estimation des propriétés mécaniques puisque la raideur de contact est déterminée à partir de la pente de la courbe d’indentation au début de décharge. Pour éviter des erreurs notables sur l’évaluation des caractéristiques mécaniques, Chadoba et Richter [96] proposent de maintenir la force maximale pendant une période de 10 à 60 secondes avant la décharge afin de limiter l’influence du fluage.
Figure III.6. Représentation du fluage au début de la décharge
III.4.4 Méthode de Field et Swain
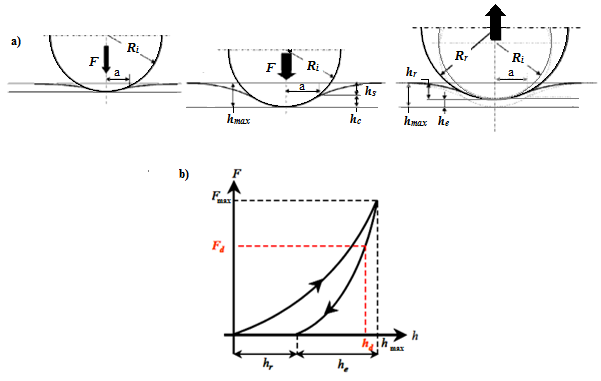
Field et Swain ont développé une méthode d’analyse de la courbe d’indentation [97] qui reste valable que pour le cas d’indentation sphérique. Cette approche vise comme le modèle d’Oliver et Pharr, à découpler les contributions élastiques et plastiques, afin d’utiliser les équations de Hertz [80,81] pour calculer la profondeur de déformation plastique et par conséquent calculer d’une façon directe la dureté et le module d’élasticité du matériau indenté.
Au cours de l’indentation d’un échantillon, il peut y avoir une réponse élastique aux faibles charges, suivie de déformation élastoplastique aux charges plus élevées. On peut facilement admettre que si la charge Fmax, atteinte à une profondeur maximale hmax après un cycle total (charge-décharge) d’indentation, est réappliquée sur l’échantillon indenté, le matériau se déforme élastiquement avec une profondeur élastique he; lorsque la charge est enlevée, la même empreinte résiduelle du cycle précédent demeure avec une profondeur :
Ainsi en utilisant les équations de contact sphère/plan de Hertz [3,4], Field et Swain établissent l’expression suivante :
Où Er est le module élastique réduit, F est la charge appliquée, a est le rayon du cercle de contact et hmax et hr correspondent respectivement aux profondeurs d’indentation maximale et résiduelle.
Comme dans le modèle d’Oliver et Pharr, Field et Swain définissent la profondeur de déformation plastique hc comme étant la différence entre la profondeur maximale hmax et la déflexion élastique hs où ils considèrent que la décharge à partir de la profondeur hmax jusqu’à la profondeur résiduelle hr est purement élastique (figure III.7).
Les équations d’Hertz pour un contact sphère/plan, montrent que la distance séparant la surface libre du matériau au cercle de contact (déflexion hs) est égale à la moitié de la profondeur élastique he. On obtient ainsi l’équation suivante :
On peut donc exprimer des expressions (10), (12) et (14), la profondeur de contact en fonction des profondeurs maximale et résiduelle qui peuvent être mesurées expérimentalement (eq.15).
Une fois que la profondeur de contact hc est déterminée, il est facile, dans le cas d’une pointe sphérique de rayon R, de calculer le rayon de contact a à partir de l’équation (16) et déterminer par la suite l’aire de contact Ac.
Puisque les profondeurs hmax et hr sont mesurables expérimentalement, il est alors facile, d’une part de calculer he (eq.13) et par la suite déterminer le module de Young à partir des relations (14) et (2) et d’autre part, d’obtenir l’aire de contact (eq.16 et 17) permettant d’évaluer la dureté du matériau.
Cette procédure ne garantit pas une mesure précise puisque la mesure expérimentale de la profondeur résiduelle peut être biaisée par le fait que les contraintes résiduelles peuvent entraîner des relaxations plastiques dans le matériau [97].
Figure III.7. a) Configuration du contact sphère/plan, b) Courbe d’indentation de Field et Swain.
Field et Swain font l’hypothèse suivante: le comportement d’un matériau homogène en réponse d’une décharge partielle à partir de la charge maximale Fmax jusqu’à une charge partielle Fd est similaire à une réponse élastique à la suite d’un chargement de Fd à Fmax (figure III.7.b).
Étant donné que l’essai de nanoindentation donne directement les valeurs de charges appliquées et profondeurs correspondantes, cette réponse élastique peut être calculée par l’intermédiaire des équations d’Hertz suivantes:
Ainsi un simple calcul du rapport du déplacement élastique obtenu à chargement maximal Fmax sur celui évalué à chargement partiel Fd, aboutit d’une manière précise à la profondeur résiduelle comme suit :
III.4.5 Limitation de la méthode de Field et Swain
Les équations de Hertz mis en évidence dans l’approche de Field et Swain [97] sont fondées sur des hypothèses où la profondeur d’indentation est très petite devant le rayon de contact (h<
Une importante incertitude de l’approche de Field et Swain est liée à la charge partielle qui doit être purement élastique. En effet, si cette charge est suffisamment élevée pour induire de nouveau une déformation plastique dans le matériau, la valeur calculée de la profondeur résiduelle hr mène à une fausse évaluation des caractéristiques recherchées. D’autre part, une charge partielle très petite augmente les erreurs de calcul du fait de l’augmentation de l’incertitude associée aux instruments de mesure.
III.5 Caractérisation par la méthode dynamique
Comme expliqué ci-dessus, ce qui limite le modèle statique d’Oliver et Pharr [89] est le calcul de la raideur de contact à partir d’un seul point, au début de la décharge. Grâce à la méthode Continuous Stiffness Measurement ou mesure continue de la raideur de contact, il est possible de mesurer la raideur de contact de façon continue tout au long du déplacement de l’indenteur. C’est ce qui fait de cette méthode la plus appropriée pour l’évaluation de la dépendance entre les propriétés mécaniques et l’épaisseur des couches minces.
Figure III.8. Modèle dynamique de nanoindentation (CSM).
Dans cette configuration de nanoindentation l’indenteur est soumis à une charge sinusoïdale de pulsation constante lors de son enfoncement dans l’échantillon. Donc plusieurs cycles de charge-décharge sont imposés lors de la phase de chargement comme il est illustré dans la figure III.8. Les signaux dynamiques résultants sont analysés pour déterminer la raideur de contact dont l’expression est donnée par :
Où Kf et m sont respectivement la raideur et la masse de l’instrument d’indentation, Ks est la raideur des lames-ressorts maintenant cet instrument, F0 et z0 représentent respectivement les amplitudes de la force et du déplacement, et ɸreprésente le déphasage entre le déplacement et la charge. La modélisation ayant permis la détermination de la raideur de contact S est détaillée dans l’annexe 2.
Cette méthode permet ainsi de mesurer les propriétés mécaniques des couches de quelques centaines de nanomètres d’épaisseur, en fonction du déplacement de la pointe d’indentation. Elle permet également de s’affranchir de l’effet du fluage puisqu’il n’est pas nécessaire d’utiliser le début de la décharge où ce problème peut être rencontré.
III.6 Etude expérimentale
III.6.1 La couches étudiée
Les caractéristiques mécaniques et tribologiques de la couche déposée sont liées directement à la nature du substrat. Le revêtement à déposer dépend bien évidemment du niveau de performance qu’exige l’application envisagée. Ainsi, une convenance entre le revêtement d’un substrat donné avec le niveau de performance exigé est indispensable.
Le dépôt étudié est employé pour l’amélioration de la dureté et de la rigidité de pièces mécaniques utilisées souvent contre l’usure, ce qui nécessite l’utilisation de substrat de dureté élevée.
Le choix est porté sur l’acier 100Cr6, employé couramment dans les applications mécaniques en particulier les cages à billes des roulements. Cet acier présente une dureté d’environ 10 GPa et un module d’élasticité théorique de 200 GPa.
Le revêtement du substrat a été réalisé au sein de l’entreprise française Balzers, par une pulvérisation à magnétron sous des conditions de dépôts optimisées afin d’avoir une couche d’épaisseur de 2.7 μm, uniforme et qui présente de bonnes propriétés fonctionnelles.
III.6.2 Mesure des propriétés mécaniques par nanoindentation sur CSM
Le dispositif d’essai disponible au Laboratoire de Mécanique Matériaux et Procédés de l’École Supérieure des Sciences et Techniques de Tunis (nanoindenteur NHT-CSM) a été utilisé pour la caractérisation mécanique du revêtement WC. Des petites charges de 0.04 μN peuvent être appliquées et des déplacements de l’ordre de 0,04 nm peuvent être mesurés.
L’indenteur utilisé est de type Berkovich, les essais étant effectués sous le mode sinus mesurant la rigidité de contact en continu, permettent d’étudier l’évolution des propriétés mécaniques dans la couche.
Le dispositif permet de réaliser l’essai à force imposée. Pour cela, nous avons utilisé le chargement maximal de l’appareil (500 mN) afin d’étudier l’évolution des propriétés mécaniques dans la couche. Les autres principaux paramètres de l’essai sont :
– Vitesse de charge : 1000 mN/min;
– Fréquence : 5 Hz;
– Amplitude harmonique : 30 mN;
– Vitesse d’approche : 2000 nm/min.
L’essai de nanoindentation est par nature extrêmement sensible aux impuretés présentes dans le matériau, ainsi que la rugosité de surface. Pour cette raison, plusieurs indentations à différents endroits du revêtement ont été réalisées pour avoir une dispersion de résultats que nous étudierons la moyenne.
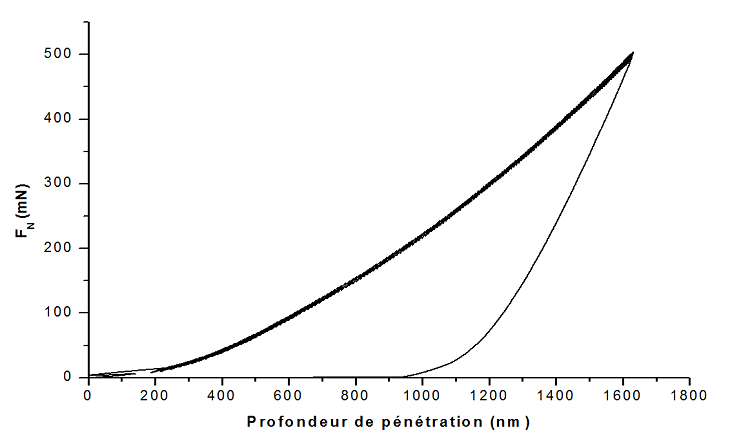
La figure III.9 représente une courbe de charge-déplacement obtenue lors des essais d’indentation. En observant cette courbe sur les premières centaines de nanomètres de pénétration, on remarque la présence d’une discontinuité entre 148 et 226 nm (figure III.9). Il s’agit de la génération de la première série de dislocations provoquant une transition brutale entre la déformation élastique pure et la déformation plastique. Ce phénomène, appelé pop-in, est étudié par plusieurs auteurs [98,99]. Il se manifeste par un enfoncement brusque de la pointe dans le matériau à une charge appliquée constante.
Figure III.9. Courbe charge-déplacement.
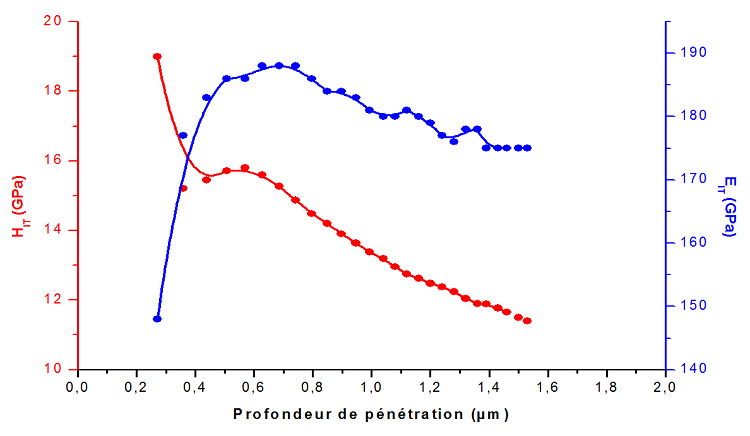
La figure III.10 illustre les profils de dureté et de module d’élasticité du revêtement. La profondeur d’indentation maximale atteinte est de 1.53 μm qui est inférieure à l’épaisseur de la couche (2.7 μm) pourtant les mesures à cette profondeur sont influencées par le substrat.
Figure III.10. Profil de dureté et de module d’élasticité par indentation sous NHT-
Le profil de dureté présente un pic entre 271 nm et 360 nm de pénétration qui correspond au brusque enfoncement généré par le pop-in. Cet enfoncement génère la croissance d’un bourrelet qui augmente l’aire de contact effectif entre l’indenteur et le matériau et conduit à une valeur de dureté élevée. À partir de ce point, on remarque un palier pour des profondeurs de pénétration comprises entre 360 nm et 650 nm, dont la dureté est à peu près constante à une valeur d’environ 15,5±0.5 GPa; celle-ci présente la dureté intrinsèque de la couche de WC. Au fur et à mesure que la profondeur augmente, la dureté diminue continuellement vers des valeurs très influencées par le substrat qui présente une dureté inférieure à celle du dépôt. On constate les mêmes ordres de dureté des couches en WC obtenue par pulvérisation magnétron dans plusieurs travaux [31,40].
Contrairement au profil de dureté, les valeurs de module augmentent très rapidement dès les plus faibles pénétrations, puis se stabilisent entre 500 nm et 796 nm à une valeur de l’ordre 185 GPa. Cette valeur correspond probablement au module d’élasticité du revêtement. Néanmoins, il est couramment supposé qu’au-delà d’une pénétration de 10 % de l’épaisseur de la couche, l’influence du substrat n’est plus négligeable pour la mesure du module de Young. Toutefois, pour des profondeurs supérieures à 796 nm, on constate que le module de Young diminue considérablement et se stabilise, dans des profondeurs inférieures à l’épaisseur de la couche, à une valeur de l’ordre de 175 GPa. Cette valeur qui correspond systématiquement au module du substrat. Ceci permet de conclure que le module de la couche est de l’ordre de 185 GPa.
III.6.3 Mesure des propriétés mécaniques par nanoindentation sur MTS
Nous avons également testé l’échantillon à l’aide d’un nanoindenteur MTS XP situé au Centre d’Enseignement et de Recherche Arts et Métiers ParisTech de Lille. Cet appareil équipé d’un indenteur Berkovich, possède une résolution de chargement et de déplacement plus grande que celle du NHT-CSM, de l’ordre de 0.1 nN et 0.1 nm respectivement, permettant de réaliser l’indentation à déplacement imposé.
Les principaux paramètres d’essai sont :
. Oscillation harmonique : 2 nm;
. Profondeur d’indentation maximale : 2000 nm;
. Chargement maximal : 650 mN;
. Vitesse d’approche à la surface : 10 nm/s;
. Fréquence : 45 Hz.
Les résultats obtenus sont reportés sur la figure IV.11.
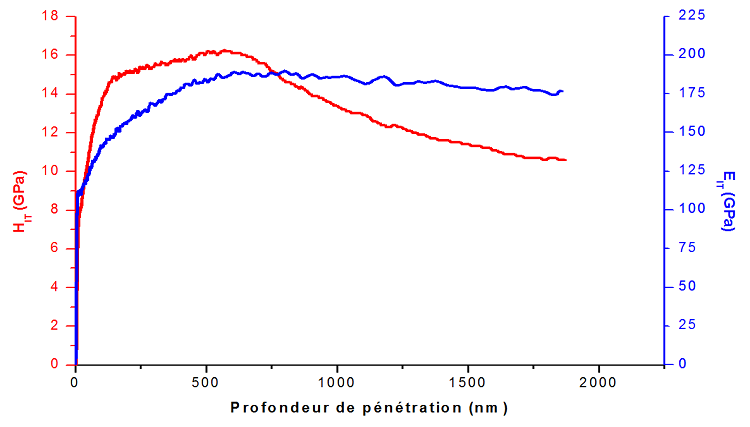
Figure III.11. Profil de dureté et de module d’élasticité par indentation sous MTS-XP.
On remarque que le profil de dureté croit continuellement et se stabilise à une valeur de 15,5±0.5 GPa pour une profondeur de pénétration comprise entre 120 et 850 nm. Puis la dureté diminue pour atteindre au-delà d’une profondeur de 1400 nm, une valeur de 10 GPa environ qui est identique à la dureté théorique de l’acier 100Cr6 en occurrence du substrat. La dureté de la couche est ainsi égale à 15,5±0.5 GPa.
Il est important de remarquer qu’il est beaucoup plus difficile d’estimer le module élastique de la couche étudiée indépendamment des propriétés du substrat. La déformation élastique s’étend en effet sur une profondeur de l’échantillon beaucoup plus grande que celle où s’étend la déformation plastique.
Les valeurs de module tracées en fonction de la profondeur augmentent rapidement, des valeurs de l’ordre de 190 GPa plus ou moins stables jusqu’à une profondeur de 1400 nm. Une profondeur qui apparait relativement importante par rapport à l’épaisseur de 2.7 μm de la couche. Cette valeur est ainsi biaisée par le module de Young du substrat et ne peut être pas considérée comme une caractéristique du dépôt. C’est pour cette raison que le module d’élasticité est conventionnellement calculé à une profondeur de 10 % de l’épaisseur.
III.6.4 Comparaison des résultats
La différence entre les systèmes de pilotage de l’indenteur dans les deux appareils utilisés, commande l’évaluation des caractéristiques mécaniques.
L’indentation à force imposée, réalisée par le nanoindenteur NHT, fournit des mesures avec une dispersion convenable pour l’identification des caractéristiques du revêtement par rapport aux celles du substrat. Toutefois, elle présente parfois des irrégularités de mesures à cause de l’apparition du phénomène pop-in qui est liée à la charge imposée par l’indenteur et le comportement du matériau indenté.
L’indentation à pénétration imposée, que procure l’indenteur MTS-XP, permet de pallier les discontinuités de mesures générées par le phénomène pop-in par l’action de la pénétration progressive. Cette dernière, produit des bourrelets qui affectent les mesures à de faibles pénétrations, en particulier pour l’indentation des couches très minces et ductiles. Néanmoins, elle n’est pas gênante dans l’indentation de la couche étudiée dans ce travail. On constate également que la courbe du module d’élasticité est très lissée vu que les mesures sont à de pénétrations très proches. Ce qui pose un problème pour l’identification du module intrinsèque du revêtement. Par ailleurs, ce problème peut être remédié par une oscillation harmonique plus grande ou des fréquences plus petites.
III.6.5 Morphologie de la couche étudiée
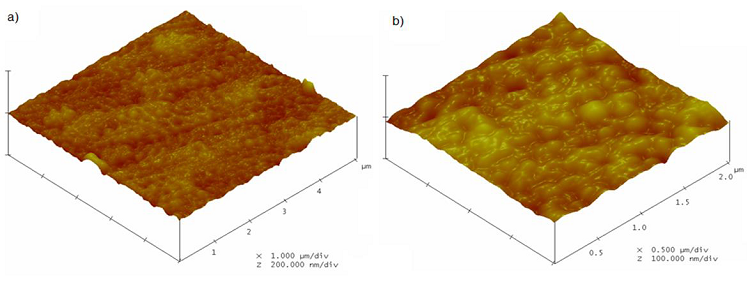
Des observations par microscope à force atomique (AFM) du dépôt étudié ont été réalisées sur un Nanoscope III au Centre National de Recherche en Sciences des Matériaux, afin d’analyser la topographie de la couche étudiée. Les images obtenues sont illustrées dans les figures III.12 et III.13.
On remarque que la topographie de la couche est globalement uniforme avec la présence de dômes d’une densité de 1.753/μm². La couche comprend également des minuscules cratères répartis sur l’ensemble de la surface.
Figure III.12. Topographie de la couche WC observée en 2D.
Les mesures dimensionnelles des dômes et cratères montrent que le diamètre moyen des dômes est environ de 95 nm alors que la profondeur maximale des cratères n’excède pas 58 nm. La différence insignifiante entre les sommets des dômes et les seuils des cratères n’affectent pas l’état de surface. Ce qui mène à un excellent état de surface, favorable pour des applications tribologiques, dont la rugosité moyenne mesurée sur 5 μm n’excède pas 8 nm.
Figure III.13. Topographie de la couche WC observée en 3D, surface observée : a) 5μm², b) 2μm².
En effet, cette topographie est observée à la zone morphologique M du modèle de Messier, présenté précédemment dans le paragraphe I.5. Cette morphologie est caractérisée par une structure fibreuse et dense, avec une dureté généralement favorable pour des applications mécaniques. Ceci vient d’être confirmé par les valeurs de dureté et de module d’élasticité que nous avons trouvé.
En comparant la morphologie de la couche étudiée aux monocouches TiN, CrN, TiAlN, CrAlN obtenues par procédé magnétron [44,46,52], on note que la couche en WC présente une structure plus homogène avec un meilleur état de surface.
III.6.6 Evaluation du coefficient de frottement
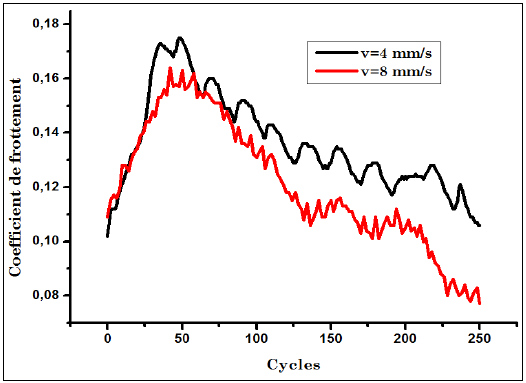
Un test tribologique bille sur disque a été effectué avec deux vitesses de glissement différentes à l’aide d’un tribo-testeur équipé d’une en WC, pour évaluer le coefficient de frottement du revêtement. Les deux essais sont réalisés à sec. La figure III.14 montre l’évolution du coefficient de frottement enregistré en fonction du nombre de cycle de rotation.
On remarque que le coefficient de frottement augmente considérablement à partir de 25 cycles pour les deux essais, ce qui correspond au début d’usure du dépôt, puis diminue continuellement. Il est à noter que si la vitesse de glissement augmente le coefficient diminue dû à la diminution de la force de frottement.
Figure III.14. Evolution du coefficient de frottement en fonction du nombre de cycles.
Le coefficient maximal atteint est de 0.175, ce qui reflète un très bon état de surface et de meilleures caractéristiques tribologiques du revêtement en WC par rapport à ceux en CrN et TiN qui présentent comme reporté dans la littérature, un coefficient de frottement aux alentours de 0.4 et 0.2 respectivement [44,61].
III.7 Conclusion
L’évaluation des propriétés mécaniques de la couche étudiée a été réalisée selon une échelle nanométrique basée sur l’essai de nanoindentation qui nous a permis, en s’appuyant sur la méthode d’Olivier et de Pharr, d’analyser le comportement du revêtement durant l’indentation et de mesurer sa dureté et son module de Young avec précision. Les résultats obtenus sont en harmonies avec la morphologie observée par l’analyse AFM et coïncide avec les attentes initiales discutées dans la bibliographie. De telles propriétés mécaniques et tribologiques sont favorables pour le revêtement des outils de coupe.
Cependant, il convient de rester très critique envers la mesure des caractéristiques mécaniques, car l’utilisation généralisée de la nano indentation, en particulier sur les couches minces, peut conduire à des erreurs importantes. Par ailleurs, l’évaluation des caractéristiques mécaniques des couches minces nécessite la maitrise de l’instrument utilisé.
En effet, le revêtement PVD en carbure de tungstène apporte une amélioration mécanique et tribologique considérable au substrat en acier 100Cr6.
Cette caractérisation mécanique permet d’éliminer rapidement les dépôts de mauvaise qualité ou qui ne correspondent pas au cahier de charge, mais ne permet pas de choisir les dépôts adaptés pour une application précise. De plus, les propriétés qu’impose l’utilisateur des pièces revêtues ne se résument pas qu’autour de la dureté, du module d’élasticité ou de l’épaisseur de la couche déposée, mais concernent aussi l’accrochage du dépôt au substrat et par la suite la durée de vie de la pièce revêtue.
C’est dans ce cadre que s’inscrit le chapitre suivant, qui s’intéresse à l’étude de l’adhérence des couches minces, en particulier, celles en carbure de tungstène.
Page suivante : Chapitre IV. Caractérisation de l’adhérence des couches minces par Scratch Test
Retour au menu : CARACTERISATION MECANIQUE ET ADHERENCE DE REVETEMENT PVD EN CARBURE DE TUNGSTENE