Dans ce présent chapitre, il est ignoré la saisonnalité du prix spot du soja négligeable et cachée par la tendance ainsi que les processus autorégressifs et moyennes mobiles, et non la stationnarité du prix anticipé au seuil de 5%.Le prix sur le marché à terme est anticipé à partir de la variation passée du prix au comptant, plus une constante, plus une erreur qui englobe les perspectives diverses identiques à des phénomènes géopolitiques, à une inflation par les coûts liés au prix du baril de pétrole, à des décisions macroéconomiques, aux risques de « réputation » liés au soja etc…..
〖logfuture〗_t=c+〖dspot〗_(t-1)+ε^future
Le prix au comptant n’est jamais loin de celui anticipé sur le marché. Compte tenu du prix anticipé, on peut dire que le prix au comptant ou sa variation est le résultat du prix anticipé en plus d’une erreur d’anticipation du prix anticipé, et une erreur d’anticipation du prix au comptant et une constante près.
〖dspot〗_t=c+〖logfuture〗_t+ε^future+ε^dspot
Estimation de :
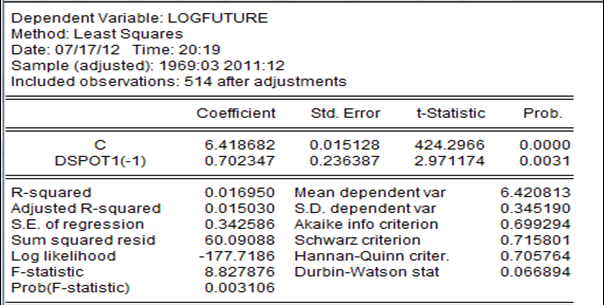
〖future〗_t=c+〖dspot〗_(t-1)+ε^future
Les écarts entre le prix anticipé et la dernière variation de prix suivie d’une constante sont auto-corrélés et hétèroscédastiques et anormaux. Nous incluons toutes ces erreurs dans la variation de prix présente.
L’estimation sous Eviews donne les résultats suivants :
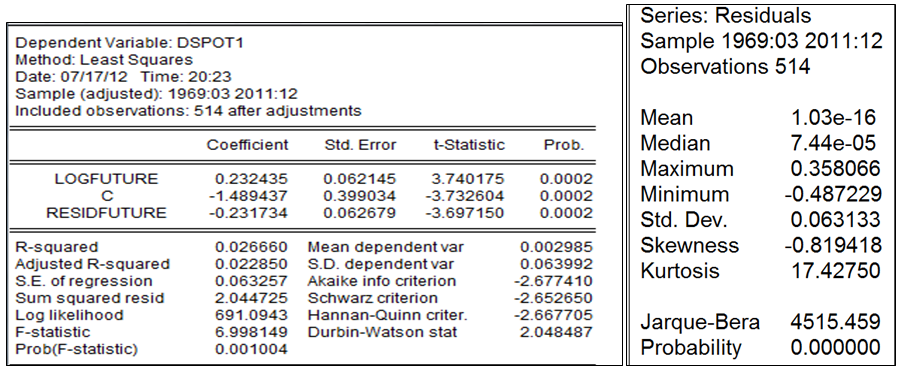
〖dspot〗_t=c+〖future〗_t+ε^future+ε^dspot
Les tests sur le corrélogramme des écarts et le corrélogramme des de ces mêmes écarts au carré montrent la présence d’auto-corrélation et d’hétéroscédasticité. Dans le cadre d’une couverture par la détermination du nombre de contrats que le producteur doit acheter, nous nous intéressons particulièrement au garch et les modèles non linéaires egarch ,tarch et tgarch.
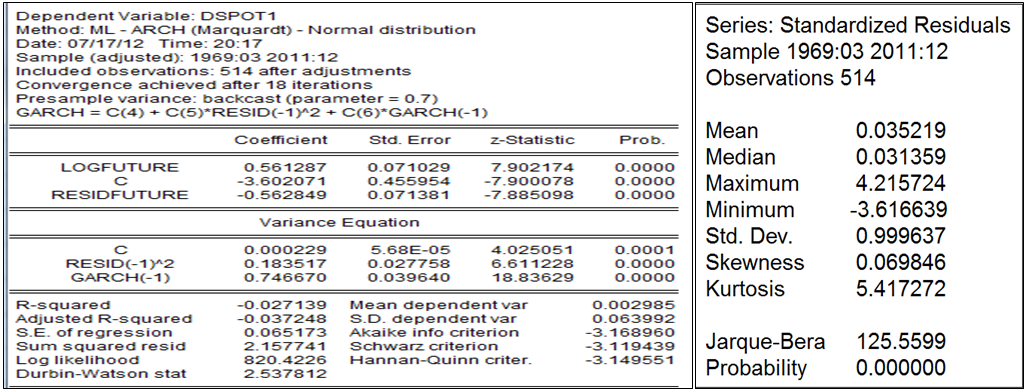
Garch(1,1)
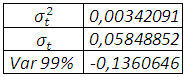
La couverture par un garch estime un taux de couverture de 56,1287%, taux auquel on peut se fier au regard des résidus non corrélés et hétéroscédastiques malgré l’épaisseur de la queue de distribution. Par la même occasion nous calculons la value at risk au seuil de 1%.
Cela dit en janvier 2012 le prix du soja ne baissera pas en dessous 13,6%.
Egarch(1,1)
L’egarch indique sensiblement le même taux de couverture de 56%, mais possède une queue plus épaisse que le garch en dépit de la non auto-corrélation et l’homoscédasticité. Ce pourquoi nous privilégions le garch.
Tarch(2,1)
Les bonnes et les mauvaises nouvelles n’ont pas le même impact sur la variance conditionnelle des rendements de prix du soja. Ce fait « stylisé » peut être approché via le modèle à seuil threshold arch et s’exprime par la relation :
σ_t^2=w+αε_(t-1)^2+γε_(t-1)^2 d_(t-1)
Avec d_t=1 si c’est une mauvaise nouvelle (ε_t
Estimation :
Le tarch suggère un taux de couverture de 77,99% contre le risque de baisse, un taux très supérieur à ceux indiqués par le garch et egarch. Nous privilégions le tarch du fait de sa queue de distribution sensiblement moins épaisse en plus de l’absence d’auto-corrélation et d’hétéroscédasticité.
σ_t^2=0.0012+0.2562ε_(t-1)^2+ 0.2561ε_(t-1)^2 d_(t-1)+〖0.3629ε〗_(t-2)^2
On peut calculer la value at risk :
Avec un taux de couverture de 77,99%, le risque de baisse de prix se ramène à 9,39% à l’horizon d’un mois. La couverture par les modèles économétriques se voit pour la plupart du temps heurtée à l’épaisseur de queue des distributions. Ce problème peut être abordé via les outils de mesure de risque moins restrictifs que l’écart-type ou la variance, en nous intéressant de façon intrinsèque aux rendements à la fois du prix anticipé mensuel et du prix au comptant mensuel du soja, quoi que le prix anticipé soit stationnaire ou non, ce qui fait l’objet du prochain chapitre.
Page suivante : Section 2: Couverture par les mesures de risques
Retour au menu : La couverture des produits agricoles sur les marchés à terme : Cas du soja